题目内容
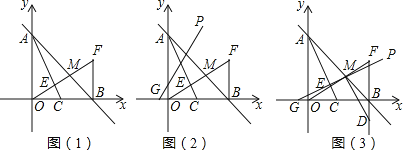
【题目】如图(1),在平面直角坐标系中,直线y=-x+m交y轴于点A,交x轴于点B,点C为OB的中点,作C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
(1)直接写出点F的坐标(用m表示);
(2)求证:OF⊥AC;
(3)如图(2),若m=2,点G的坐标为(-![]() ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
①求k的取值范围;
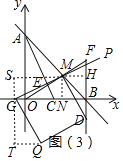
②如图(3),若直线GP经过点M,过点M作GM的垂线交FB的延长线于点D,在平面内是否存在点Q,使四边形DMGQ为正方形?如果存在,请求出Q点坐标;如果不存在,请说明理由.
【答案】(1)(m,![]() m)(2)见解析(3)①0<k<6②(
m)(2)见解析(3)①0<k<6②(![]() ,-
,-![]() )
)
【解析】
(1)CF⊥AB,CR=FR,则∠RCB=45°,则RC=RB=RF,∠RBF=45°,即FB⊥x轴,即可求解;
(2)证明△AOC≌△OBF(HL),即可求解;
(3)①将点(-![]() ,0)代入y=kx+b即可求解;②求出点D(2,-1),证明△MNG≌△MHD(HL),即可求解.
,0)代入y=kx+b即可求解;②求出点D(2,-1),证明△MNG≌△MHD(HL),即可求解.
解:(1)y=-x+m,令x=0,则y=m,令y=0,则x=m,则∠ABO=45°,
故点A、B的坐标分别为:(0,m)、(m,0),则点C(![]() m,0),
m,0),
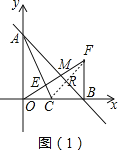
如图(1)作点C的对称轴F交AB于点R,则CF⊥AB,CR=FR,
则∠RCB=45°,则RC=RB=RF,
∴∠RBF=45°,即FB⊥x轴,
故点F(m,![]() m);
m);
(2)∵OC=BF=![]() m,OB=OA,
m,OB=OA,
∴△AOC≌△OBF(HL),
∴∠OAC=∠FOB,
∵∠OAC+∠AOE=90°,
∴∠OAC+∠AOE=90°,
∴∠AEO=90°,
∴OF⊥AC;
(3)①将点(-![]() ,0)代入y=kx+b得:
,0)代入y=kx+b得:
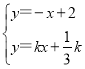 ,解得:
,解得: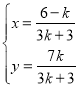 ,
,
由一次函数图象知:k>0,
∵交点在第一象限,则 ,
,
解得:0<k<6;
②存在,理由:
直线OF的表达式为:y=![]() x,直线AB的表达式为:y=-x+2,
x,直线AB的表达式为:y=-x+2,
联立上述两个表达式并解得:x=![]() ,故点M(
,故点M(![]() ,
,![]() ),
),
直线GM所在函数表达式中的k值为:![]() ,则直线MD所在直线函数表达式中的k值为-
,则直线MD所在直线函数表达式中的k值为-![]() ,
,
将点M坐标和直线DM表达式中的k值代入一次函数表达式并解得:
直线DM的表达式为:y=-![]() x+4,故点D(2,-1),
x+4,故点D(2,-1),
过点M作x轴的垂线于点N,作x轴的平行线交过点G于y轴的平行线于点S,
过点G作y轴的平行线交过点Q与x轴的平行线于点T,
则![]() ,
,
∴△MNG≌△MHD(HL),
∴MD=MG,
则△GTQ≌△MSG,则GT=MS=GN=![]() ,TQ=SG=MN=
,TQ=SG=MN=![]() ,
,
故点Q(![]() ,-
,-![]() ).
).

【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?