ЬтФПФкШн
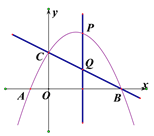
ЁОЬтФПЁПШчЭМ,дкЦНУцжБНЧзјБъЯЕжа,вЛДЮКЏЪ§yЃН![]() xЃЋ2ЕФЭМЯѓгыxжсНЛгкЕуA,гыyжсНЛгкЕуC,ХзЮяЯпyЃНax2ЃЋbxЃЋcЙигкжБЯпxЃН
xЃЋ2ЕФЭМЯѓгыxжсНЛгкЕуA,гыyжсНЛгкЕуC,ХзЮяЯпyЃНax2ЃЋbxЃЋcЙигкжБЯпxЃН![]() ЖдГЦЃЌЧвОЙ§A. CСНЕуЃЌгыxжсНЛгкСэвЛЕуЮЊB.
ЖдГЦЃЌЧвОЙ§A. CСНЕуЃЌгыxжсНЛгкСэвЛЕуЮЊB.
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ШєЕуPЮЊжБЯпACЩЯЗНЕФХзЮяЯпЩЯЕФвЛЕу,Й§ЕуPзїPQЁЭxжсгкMЃЌНЛACгкQЃЌЧѓPQЕФЁЭзюДѓжЕЃЌВЂЧѓДЫЪБЁїAPCЕФУцЛ§ЃЛ
(3)дкХзЮяЯпЕФЖдГЦжсЩЯевГіЪЙЁїADCЮЊжБНЧШ§НЧаЮЕФЕуD,жБНгаДГіЕуDЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() x2ЃЋ
x2ЃЋ![]() xЃЋ2ЃЛ(2)4ЃЛЃЈ3ЃЉDЕуЕФзјБъЮЊ(
xЃЋ2ЃЛ(2)4ЃЛЃЈ3ЃЉDЕуЕФзјБъЮЊ(![]() ,5)ЃЌ(
,5)ЃЌ(![]() ,5)ЃЌ(
,5)ЃЌ(![]() ,1ЃЋ
,1ЃЋ![]() )ЃЌ(
)ЃЌ(![]() ,1Ѓ
,1Ѓ![]() ).
).
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉгЩжБЯпЙ§ЕуAЃЌПЩЕУГіЕуAЕФзјБъЃЌгЩAЁЂBЙигкжБЯпx=![]() ЖдГЦПЩевГіBЕуЕФзјБъЃЎгЩжБЯпОЙ§ЕуCПЩЧѓГіЕуCЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЖдГЦПЩевГіBЕуЕФзјБъЃЎгЩжБЯпОЙ§ЕуCПЩЧѓГіЕуCЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпACЕФНтЮіЪНЮЊy=-![]() x+2ЃЌМД
x+2ЃЌМД![]() x+y-2=0ЃЌЩшЕуQЕФзјБъЮЊЃЈmЃЌ-
x+y-2=0ЃЌЩшЕуQЕФзјБъЮЊЃЈmЃЌ-![]() m+2ЃЉЃЛдђPЕузјБъЮЊЃЈmЃЌ-
m+2ЃЉЃЛдђPЕузјБъЮЊЃЈmЃЌ-![]() m2+
m2+![]() m+2ЃЉЃЌгЩДЫЕУЕНPQ=-
m+2ЃЉЃЌгЩДЫЕУЕНPQ=-![]() ЃЈm-2ЃЉ2+2ЃЌгЩЖўДЮКЏЪ§зюжЕЕФЧѓЗЈЕУЕНЃКЕуPЃЈ2ЃЌ3ЃЉЃЌгЩЗжИюЗЈЧѓЕУЃКSЁїPAC=SЬнаЮOCPM+SЁїPMA-SЁїAOCЃЛ
ЃЈm-2ЃЉ2+2ЃЌгЩЖўДЮКЏЪ§зюжЕЕФЧѓЗЈЕУЕНЃКЕуPЃЈ2ЃЌ3ЃЉЃЌгЩЗжИюЗЈЧѓЕУЃКSЁїPAC=SЬнаЮOCPM+SЁїPMA-SЁїAOCЃЛ
ЃЈ3ЃЉМйЩшДцдкЃЌЩшГіDЕузјБъЃЌЁїADCЮЊжБНЧШ§НЧаЮЗжШ§жжЧщПіЃК
ЂйЕБЕуCЮЊжБНЧЖЅЕуЪБЃКзїDMЁЭyжсгкMгЩЁїCD1MЁзЁїACOПЩЕУЃКCM=3ЃЌЫљвдOM=5ЃЌМДD1ЃЈ![]() ЃЌ5ЃЉЃЛ
ЃЌ5ЃЉЃЛ
ЂкЭЌРэЕБЕуAЮЊжБНЧЖЅЕуЪБПЩЧѓD2ЃЈ![]() ЃЌ-5ЃЉЃЛ
ЃЌ-5ЃЉЃЛ
ЂлЕБЕуDЮЊжБНЧЖЅЕуЪБЃКЙ§D3зїMNЁЭyжсЃЎгЩЁїCD3MЁзЁїD3NAПЩЕУЃКn2-2n=![]() ЃЎвзЕУD3ЃЈ
ЃЎвзЕУD3ЃЈ![]() ,1ЃЋ
,1ЃЋ![]() ЃЉЃЌD4ЃЈ
ЃЉЃЌD4ЃЈ![]() ,1Ѓ
,1Ѓ![]() ЃЉЃЎ
ЃЉЃЎ
ЯъНтЃК(1)СюyЃН![]() xЃЋ2ЃН0ЃЌНтЕУЃКxЃН4ЃЌ
xЃЋ2ЃН0ЃЌНтЕУЃКxЃН4ЃЌ
МДЕуAЕФзјБъЮЊ(4,0).
ЁпAЁЂBЙигкжБЯпxЃН![]() ЖдГЦЃЌ ЁрЕуBЕФзјБъЮЊ(1,0).
ЖдГЦЃЌ ЁрЕуBЕФзјБъЮЊ(1,0).
СюxЃН0ЃЌдђyЃН2ЃЌ
ЁрЕуCЕФзјБъЮЊ(0,2)ЃЌ
ЁпХзЮяЯпyЃНax2ЃЋbxЃЋcОЙ§ЕуAЁЂ BЁЂCЃЌ
Ёрга НтЕУЃК aЃН
НтЕУЃК aЃН![]() ЃЌbЃН
ЃЌbЃН![]() ЃЌcЃН2.
ЃЌcЃН2.
ЙЪХзЮяЯпНтЮіЪНЮЊyЃН![]() x2ЃЋ
x2ЃЋ![]() xЃЋ2
xЃЋ2
(2)жБЯпACЕФНтЮіЪНЮЊyЃНЃ![]() xЃЋ2,МД
xЃЋ2,МД![]() xЃЋy2ЃН0ЃЌ
xЃЋy2ЃН0ЃЌ
ЩшЕуQЕФзјБъЮЊ(mЃЌЃ![]() mЃЋ2) ЃЛдђPЕузјБъЮЊ(m,
mЃЋ2) ЃЛдђPЕузјБъЮЊ(m, ![]() m2ЃЋ
m2ЃЋ![]() mЃЋ2)ЃЌ
mЃЋ2)ЃЌ
ЁрPQЃНЃЈ![]() m2ЃЋ
m2ЃЋ![]() mЃЋ2ЃЉЃЃЈЃ
mЃЋ2ЃЉЃЃЈЃ![]() mЃЋ2ЃЉ
mЃЋ2ЃЉ
ЃН![]() m2ЃЋ2mЃНЃ
m2ЃЋ2mЃНЃ![]() ЃЈmЃ2ЃЉ2ЃЋ2
ЃЈmЃ2ЃЉ2ЃЋ2
ЁрЕБmЃН2ЪБЃЌPQзюДѓЃН2
ДЫЪБЕуPЃЈ2,3ЃЉSЁїPACЃНSЬнаЮOCPMЃЋSЁїPMAЃSЁїAOCЃН5ЃЋ3Ѓ4ЃН4
(3)МйЩшДцдк,ЩшDЕуЕФзјБъЮЊ(![]() ,5)ЃЌ(
,5)ЃЌ(![]() ,5)ЃЌ(
,5)ЃЌ(![]() ,1ЃЋ
,1ЃЋ![]() )ЃЌ(
)ЃЌ(![]() ,1Ѓ
,1Ѓ![]() ).
).
НтЗЈШчЯТЃКЩшDЕуЕФзјБъЃЈ![]() ЃЌmЃЉ
ЃЌmЃЉ
ЁїADCЮЊжБНЧШ§НЧаЮЗжШ§жжЧщПіЃК
ЂйЕБЕуCЮЊжБНЧЖЅЕуЪБЃКзїDMЁЭyжсгкM
гЩЁїCD1MЁзЁїACOПЩЕУЃК![]()
Ёр![]() ,CMЃН3 ЁрOMЃН5МДD1ЃЈ
,CMЃН3 ЁрOMЃН5МДD1ЃЈ![]() ,5ЃЉ
,5ЃЉ
ЂкЭЌРэЕБЕуAЮЊжБНЧЖЅЕуЪБПЩЧѓD2(![]() ,5)
,5)
ЂлЕБЕуDЮЊжБНЧЖЅЕуЪБ:
Й§D3зїMNЁЭyжс
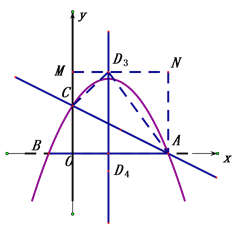
гЩЁїCD3MЁзЁїD3NAПЩЕУЃК![]()
Ёр ЃЌПЩЕУЃКn2Ѓ2nЃН
ЃЌПЩЕУЃКn2Ѓ2nЃН![]()
НтЕУЃКnЃН1ЁР![]()
D3(![]() ,1ЃЋ
,1ЃЋ![]() ),D4(
),D4(![]() ,1Ѓ
,1Ѓ![]() )
)
ЙЪDЕуЕФзјБъЮЊ(![]() ,5)ЃЌ(
,5)ЃЌ(![]() ,5)ЃЌ(
,5)ЃЌ(![]() ,1ЃЋ
,1ЃЋ![]() )ЃЌ(
)ЃЌ(![]() ,1Ѓ
,1Ѓ![]() ).
).

ЁОЬтФПЁПТЖТЖМвРяаТЙКНјСЫвЛЬЈЕчШШЫЎЦїЃЌЫ§ЖдЕчШШЫЎЦїЕФЙЄзїдРэГфТњКУЦц.ВщдФЫЕУїЪщЕУжЊЃЌЕчШШЫЎЦїЩЯУцЯдЪОЕФЮТЖШЮЊФкВПЫЎЯфжаЫЎЕФЮТЖШЃЌУПДЮМгШШЧАПЩвддЄЩшЮТЖШжЕЃЌЕБЕчШШЫЎЦїДяЕНдЄЩшЮТЖШКѓЃЌЕчШШЫЎЦїНЋЭЃжЙМгШШЃЌПЊЦєБЃЮТЙІФм.ЖјдкЪЙгУЙ§ГЬжаЃЌЕчШШЫЎЦїЛсздЖЏМгЫЎЃЌЫЎЮТЛсЯТНЕ.
ТЖТЖЗЂЯжЕчШШЫЎЦїжаЫЎЯфЕФЮТЖШyЃЈЕЅЮЛЃКЁцЃЉгыНгЭЈЕчдДКѓЕФЪБМфxЃЈЕЅЮЛЃКminЃЉжЎМфДцдкКЏЪ§ЙиЯЕЃЌЫ§ДђПЊЕчШШЫЎЦїЕФПЊЙиЃЌдЄЩшЮТЖШЮЊ70ЁцЃЌВЂМЧТМЫЎЮТБфЛЏЕФЧщПіМћЯТБэЃЌЦфжадкНгЭЈЕчдДКѓЕФЕк8minЪБЃЌЕчШШЫЎЦїДяЕНдЄЩшЮТЖШЃЛЕк18minЪБЃЌТшТшПЊЪМЪЙгУЕчШШЫЎЦї.
ЪБМфxЃЈЕЅЮЛЃКminЃЉ | 0 | 2 | 4 | 6 | 8 | 18 | 20 | 21 | 25 | 28 |
ЮТЖШyЃЈЕЅЮЛЃКЁцЃЉ | 30 | 40 | 50 | 60 | 70 | 70 | 63 | m | 50.4 | 45 |
ЃЈ1ЃЉmЕФжЕЮЊ_________ЃЛ
ЃЈ2ЃЉЧыдкЯТУцЕФзјБъЯЕжаУшГіЩЯБэжаЫљгаЪ§ОнЖдгІЕФЕуЃЌВЂИљОнУшГіЕФЕуЃЌЛГіЕБ![]() ЪБЃЌЮТЖШyЫцЪБМфxБфЛЏЕФКЏЪ§ЭМЯѓЃЛ
ЪБЃЌЮТЖШyЫцЪБМфxБфЛЏЕФКЏЪ§ЭМЯѓЃЛ

ЃЈ3ЃЉдкТЖТЖЕФТшТшЪЙгУЕчШШЫЎЦїЧАЃЌЕчШШЫЎЦїДІгкБЃЮТЙІФмЕФЪБГЄЮЊ__________minЃЛ
ЃЈ4ЃЉЮДМгШШЧАЃЌЕчШШЫЎЦїЕФЫЎЯфжаЫЎЕФЮТЖШЮЊ_________Ёц.



