Question

【题目】在Rt△ABC中，∠B=60°，BC=3，D为BC边上的三等分点，BD=2CD，E为AB边上一动点，将△DBE沿DE折叠到△DB′E的位置，连接AB′，则线段AB′的最小值为：___________．

Answer 1

【答案】

【解析】

画出图形，由折叠的性质得出BD=B′D，由三角形的三条边的数量关系得AB′＞AD-B′D，即AB′＞AD-BD，推出△DBE沿DE折叠B点落在AD上时，AB′=AD-BD，此时A′B最小，由三角函数求出AC=BCtan60°=3，由勾股定理求出AD，即可得出结果．

如图所示：

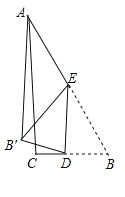
∵△DBE沿DE折叠到△DB′E，
∴BD=B′D，
∵在△AB′D中，AB′＞AD-B′D，
∴AB′＞AD-BD，
∴△DBE沿DE折叠B点落在AD上时，AB′=AD-BD，此时A′B最小，
∵在Rt△ABC中，∠B=60°，BC=3，
∴AC=BCtan60°=3，

∵BD=2CD，
∴CD=1，BD=2，
由勾股定理得：AD＝，

∴A′B=AD-BD=.

故答案是：