题目内容
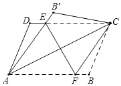
【题目】如图，现将平行四边形ABCD沿其对角线AC折叠，使点B落在点B′处．AB′与CD交于点E．
（1）求证：△AED≌△CEB′；
（2）过点E作EF⊥AC交AB于点F，连接CF，判断四边形AECF的形状并给予证明．
【答案】（1）见解析（2）见解析
【解析】
（1）由题意可得AD=BC=B'C，∠B=∠D=∠B'，且∠AED=∠CEB'，利用AAS证明全等，则结论可得；
（2）由△AED≌△CEB′可得AE=CE，且EF⊥AC，根据等腰三角形的性质可得EF垂直平分AC，∠AEF=∠CEF．即AF=CF，∠CEF=∠AFE=∠AEF，可得AE=AF，则可证四边形AECF是菱形．
证明：（1）∵四边形ABCD是平行四边形
∴AD＝BC，CD∥AB，∠B＝∠D
∵平行四边形ABCD沿其对角线AC折叠
∴BC＝B'C，∠B＝∠B'
∴∠D＝∠B'，AD＝B'C且∠DEA＝∠B'EC
∴△ADE≌△B'EC
（2）四边形AECF是菱形
∵△ADE≌△B'EC
∴AE＝CE
∵AE＝CE，EF⊥AC
∴EF垂直平分AC，∠AEF＝∠CEF
∴AF＝CF
∵CD∥AB
∴∠CEF＝∠EFA且∠AEF＝∠CEF
∴∠AEF＝∠EFA
∴AF＝AE
∴AF＝AE＝CE＝CF
∴四边形AECF是菱形
练习册系列答案
相关题目
【题目】我们知道不等式的两边加（或减）同一个数（或式子），不等号的方向不变．不等式组是否也具有类似的性质呢？请解答下列问题．
（1）完成下列填空：
已知 | 用“＜”或“＞”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
（2）一般地，如果
那么a+c_____b+d（用“＜”或“＞”填空）．请你说明上述性质的正确性．
