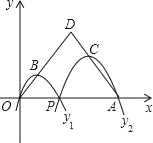
题目内容
【题目】如果a:b=b:c,即b2=ac,则b叫a和c的比例中项,或等比中项.若一个三角形一条边是另两条边的等比中项,我们把这个三角形叫做等比三角形.
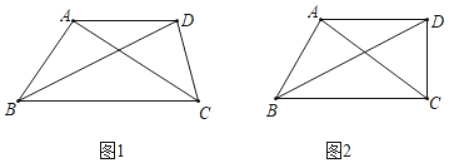
(1)已知△ABC是等比三角形,AB=2,BC=3.请直接写出所有满足条件的AC的长;
(2)如图,在四边形ABCD中,AD∥BC,对角线BD平分∠ABC,∠BAC=∠ADC,求证:△ABC是等比三角形;
(3)如图2,在(2)的条件下,当∠ADC=90时,求![]() 的值.
的值.
【答案】(1)AC=![]() 或
或![]() 或
或![]() 时,△ABC是比例三角形;(2)见解析;(3)
时,△ABC是比例三角形;(2)见解析;(3)![]() .
.
【解析】
(1)根据题目中定义的等比三角形求解即可,应分三种情况讨论;
(2)根据题意可先证明△ABC∽△DCA,从而可得CA2=BCAD,再根据已知条件证明AB=AD,从而可证明CA2=BCAB,继而△ABC是等比三角形得证;
(3)过点A作AH⊥BD于点H,由等腰三角形的性质可得BH=![]() BD,根据题意可证△ABH∽△DBC,从而可得ABBC=
BD,根据题意可证△ABH∽△DBC,从而可得ABBC=![]() BD2,由(2)的结论可得
BD2,由(2)的结论可得![]() BD2=AC2,进而可求
BD2=AC2,进而可求![]() 的值.
的值.
解:(1)∵△ABC是比例三角形,且AB=2、BC=3,
①当AB2=BCAC时,得:4=3AC,解得:AC=![]() ;
;
②当BC2=ABAC时,得:9=2AC,解得:AC=![]() ;
;
③当AC2=ABBC时,得:AC2=6,解得:AC=![]() (负值舍去);
(负值舍去);
所以当AC=![]() 或
或![]() 或
或![]() 时,△ABC是等比三角形;
时,△ABC是等比三角形;
(2)∵AD∥BC,
∴∠ACB=∠CAD,
又∵∠BAC=∠ADC,
∴△ABC∽△DCA,
∴![]() ,即CA2=BCAD,
,即CA2=BCAD,
∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴CA2=BCAB,
∴△ABC是等比三角形;
(3)如图,过点A作AH⊥BD于点H,
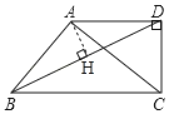
∵AB=AD,
∴BH=![]() BD,
BD,
∵AD∥BC,∠ADC=90°,
∴∠BCD=90°,
∴∠BHA=∠BCD=90°,
又∵∠ABH=∠DBC,
∴△ABH∽△DBC,
∴![]() ,即ABBC=BHDB,
,即ABBC=BHDB,
∴ABBC=![]() BD2,
BD2,
又∵ABBC=AC2,
∴![]() BD2=AC2,
BD2=AC2,
∴![]() =
=![]() .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案