题目内容
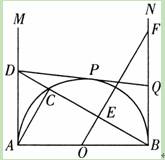
如图，在Rt△ABC中，∠C＝90°．BE平分∠ABC交AC于点E，点D在AB上，DE⊥BE于点E．
（1）判断直线AC与△DBE外接圆的位置关系，并证明你的结论；
（2）
若AD＝6，AE＝6，求BC的长．
（1）判断直线AC与△DBE外接圆的位置关系，并证明你的结论；
（2）
若AD＝6，AE＝6，求BC的长．解：（1）∵
DE⊥BE于E，∴BD为△DBE外接圆的直径，设圆心为O，
连结OE，得OE＝OB，
∴∠OBE ＝∠OEB，∵BE平分∠ABC
∴∠CBE ＝∠OBE，∴∠OEB＝∠CBE，
∴BC∥OE，已知∠C＝90°，∴∠OEC＝90°，
即直线AC是△DBE外接圆的切线．……………5分
（2）设OE＝OD＝x，在直角三角形AEO中，
AO 2＝AE 2＋EO 2，即 (6＋ x) 2＝(6) 2＋ x 2，
解得x＝3，由△ABC～△AOE，得＝，即＝，BC＝4．……………10分
DE⊥BE于E，∴BD为△DBE外接圆的直径，设圆心为O，连结OE，得OE＝OB，
∴∠OBE ＝∠OEB，∵BE平分∠ABC
∴∠CBE ＝∠OBE，∴∠OEB＝∠CBE，
∴BC∥OE，已知∠C＝90°，∴∠OEC＝90°，
即直线AC是△DBE外接圆的切线．……………5分
（2）设OE＝OD＝x，在直角三角形AEO中，
AO 2＝AE 2＋EO 2，即 (6＋ x) 2＝(6) 2＋ x 2，
解得x＝3，由△ABC～△AOE，得＝，即＝，BC＝4．……………10分
略
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(1)求证： ；
，求OD的长度．
的半径为
，圆心
的距离为
，则直线
) 
,求BC的长.