题目内容
已知:如图,AB=AC,以AB为直径的⊙O交BC于点D,过D作DE⊥AC于点E.

(1) 求证:DE是⊙O的切线;
(2)如果⊙O的半径为2,sin∠B=
 ,求BC的长.
,求BC的长.(1)证明略
(2)4
(1) 证明:连结OD,AD.
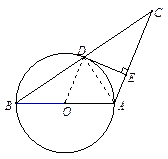
∵ AB是⊙O的直径,
∴ ∠ADB=90°………………………………1分
∴ AD⊥BC.
∵ AB=AC,
∴ BD=DC.
∵ OA=OB,
∴ OD是△ABC的中位线. ………………………………………….…………2分.
∴ OD∥AC.
∵ DE⊥AC,
∴ OD⊥DE.
∴ DE是⊙O的切线………………………………………………………………3分.
(2) 解:∵sin∠B= ,
,
∴∠B =30°.
∵ AB=4,
∴ BD=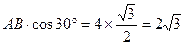 ………………………………………………4分
………………………………………………4分
∵ BD=DC.
∴ BC =4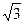 . ………………………………………………………………………5分
. ………………………………………………………………………5分

∵ AB是⊙O的直径,
∴ ∠ADB=90°………………………………1分
∴ AD⊥BC.
∵ AB=AC,
∴ BD=DC.
∵ OA=OB,
∴ OD是△ABC的中位线. ………………………………………….…………2分.
∴ OD∥AC.
∵ DE⊥AC,
∴ OD⊥DE.
∴ DE是⊙O的切线………………………………………………………………3分.
(2) 解:∵sin∠B=
 ,
, ∴∠B =30°.
∵ AB=4,
∴ BD=
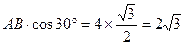 ………………………………………………4分
………………………………………………4分∵ BD=DC.
∴ BC =4
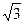 . ………………………………………………………………………5分
. ………………………………………………………………………5分
练习册系列答案
相关题目
 若AD=6,AE=6,求BC的长.
若AD=6,AE=6,求BC的长.
 内含于⊙
内含于⊙ ,⊙
,⊙ 切⊙
切⊙ ,且
,且 .若阴影部分的面积为16π,则弦
.若阴影部分的面积为16π,则弦

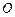 为正方形
为正方形 对角线AC上一点,以
对角线AC上一点,以 长为半径的⊙
长为半径的⊙ 相切于点
相切于点 .
.
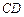 与⊙
与⊙