题目内容
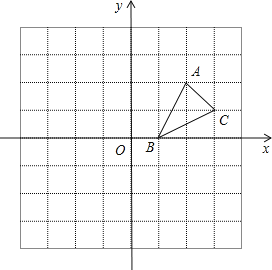
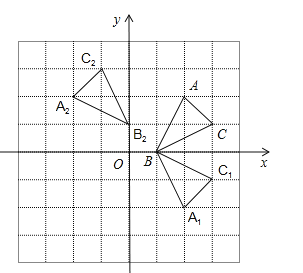
【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，
的顶点均在格点上，三个顶点的坐标分别为
.
（1）将关于
轴作轴对称变换得
，则点
的坐标为______.
（2）将绕原点
按逆时针方向旋转
得
，则点
的坐标为______.
（3）在（1）（2）的基础上，图中的，是中心对称图形，对称中心的坐标为______.
（4）若以点
、
、
、
为顶点的四边形为菱形，直接写出点的坐标为______.
【答案】（1）
；（2）
；（3）
；（4）
.
【解析】
（1）根据轴对称图形的性质可知点C的坐标为（3，-1）；
（2）根据旋转变换图形的性质也可求出点C2的坐标；
（3）成中心对称，连续各对称点，连线的交点就是对称中心，从而可以找出对称中心的坐标；
（4）根据菱形的判定进行求解即可.
（1）如图，
点C1的坐标为（3，-1）；
故答案为（3，-1）；
（2）点C2的坐标为（-1，3），
故答案为（-1，3）；
（3）△A1B1C1与△A2B2C2成中心对称，对称中心的坐标为
；
故答案为；
（4）∵点D、A、C、B为顶点的四边形为菱形，
∴点D的坐标为（4，3）.
故答案为（4，3）.
【题目】某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现， 销售量y（件）与销售单价x（元）符合一次函数，所调查的部分数据如表：
销售单价x（元） | 65 | 70 | 80 | … |
销售量y（件） | 55 | 50 | 40 | … |
（1）求出y与x之间的函数表达式；
（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少？
（3）销售单价定为多少元时，该商场获得的利润恰为500元？
【题目】甲、乙两组同时加工某种零件，甲组每小时加工80件，乙组加工的零件数量y（件）与时间x（小时）为一次函数关系，部分数据如下表所示．
x（小时） | 2 | 4 | 6 |
y（件） | 50 | 150 | 250 |
（1）求y与x之间的函数关系式；
（2）甲、乙两组同时生产，加工的零件合在一起装箱，每满340件装一箱，零件装箱的时间忽略不计，求经过多长时间恰好装满第1箱？
