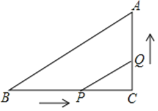
[题目]如图所示.∠C=90°.BC=8cm.AC=6cm.点P从点B出发.沿BC向点C以2cm/s的速度移动.点Q从点C出发沿CA向点A以1cm/s的速度移动.如果P.Q分别从B.C同时出发.过多少秒时.以C.P.Q为顶点的三角形恰与△ABC相似? 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，∠C=90°，BC=8cm，AC=6cm，点P从点B出发，沿BC向点C以2cm/s的速度移动，点Q从点C出发沿CA向点A以1cm/s的速度移动，如果P、Q分别从B、C同时出发，过多少秒时，以C、P、Q为顶点的三角形恰与△ABC相似？

【答案】2.4秒或秒

【解析】

设经过y秒后相似，由于没有说明对应角的关系，所以共有两种情况：△CPQ∽△CBA与△CPQ∽△CAB

设经过y秒后，△CPQ∽△CBA，此时BP=2y，CQ=y．
∵CP=BC-BP=8-2y，CB=8，CQ=y，CA=6．
∵△CPQ∽△CBA，

∴，

∴

∴y=2.4

设经过y秒后，△CPQ∽△CAB，此时BP=2y，CQ=y．

∴CP=BC-BP=8-2y．

∵△CPQ∽△CAB，

∴

∴y=

所以，经过2.4秒或者经过秒后两个三角形都相似

练习册系列答案

豫欣图书自主课堂系列答案

假期伙伴寒假大连理工大学出版社系列答案

蓝博士暑假作业甘肃少年儿童出版社系列答案

快乐暑假新疆美术摄影出版社系列答案

⑴可以围成总面积为400平方米的三个大小相同的矩形羊圈？如果能，求羊圈的边长AB，BC各为多少米?如果不能，请说明理由。

⑵可以围成总面积为640平方米的三个大小相同的矩形羊圈？如果能，求羊圈的边长AB，BC各为多少米？如果不能，请说明理由。

【题目】（本小题满分10分）如图，一次函数的图象与反比例函数（为常数，且）的图象交于A（1，a）、B两点．

（1）求反比例函数的表达式及点B的坐标；

（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．

【题目】如图，OF是∠MON的平分线，点A在射线OM上，P，Q是直线ON上的两动点，点Q在点P的右侧，且PQ=OA，作线段OQ的垂直平分线，分别交直线OF、ON交于点B、点C，连接AB、PB．

（1）如图1，当P、Q两点都在射线ON上时，请直接写出线段AB与PB的数量关系；

（2）如图2，当P、Q两点都在射线ON的反向延长线上时，线段AB，PB是否还存在（1）中的数量关系？若存在，请写出证明过程；若不存在，请说明理由；

（3）如图3，∠MON=60°，连接AP，设=k，当P和Q两点都在射线ON上移动时，k是否存在最小值？若存在，请直接写出k的最小值；若不存在，请说明理由．

【答案】（1）AB=PB；（2）存在；（3）k=0.5．

【解析】试题分析：（1）结论：AB=PB．连接BQ，只要证明△AOB≌△PQB即可解决问题；

（2）存在．证明方法类似（1）；

（3）连接BQ．只要证明△ABP∽△OBQ，即可推出=，由∠AOB=30°，推出当BA⊥OM时，的值最小，最小值为0.5，由此即可解决问题；

试题解析：解：（1）连接：AB=PB．理由：如图1中，连接BQ．

∵BC垂直平分OQ，∴BO=BQ，∴∠BOQ=∠BQO，∵OF平分∠MON，∴∠AOB=∠BQO，∵OA=PQ，∴△AOB≌△PQB，∴AB=PB．

（2）存在，理由：如图2中，连接BQ．

∵BC垂直平分OQ，∴BO=BQ，∴∠BOQ=∠BQO，∵OF平分∠MON，∠BOQ=∠FON，∴∠AOF=∠FON=∠BQC，∴∠BQP=∠AOB，∵OA=PQ，∴△AOB≌△PQB，∴AB=PB．

（3）连接BQ．

易证△ABO≌△PBQ，∴∠OAB=∠BPQ，AB=PB，∵∠OPB+∠BPQ=180°，∴∠OAB+∠OPB=180°，∠AOP+∠ABP=180°，∵∠MON=60°，∴∠ABP=120°，∵BA=BP，∴∠BAP=∠BPA=30°，∵BO=BQ，∴∠BOQ=∠BQO=30°，∴△ABP∽△OBQ，∴ =，∵∠AOB=30°，∴当BA⊥OM时，的值最小，最小值为0.5，∴k=0.5．