题目内容
在△ABC中，∠A=60°，∠B=45°，AB=3+
，求△ABC的面积（结果保留根号）．
| 3 |
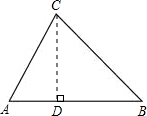
过C作CD⊥AB于D，
在Rt△ADC中，∵∠CDA=90°，
∴
=cot∠DAC=cot60°=
，
即AD=CD×
．
在Rt△BDC中，∵∠B=45°，
∴∠BCD=45°，
∴CD=BD．
∵AB=DB+DA=CD+CD×
=3+3
，
∴CD=3．
∴S△ABC=
AB×CD=
×（3+
）×3=
．
答：△ABC的面积为=
．
在Rt△ADC中，∵∠CDA=90°，
∴
| DA |
| CD |
| ||
| 3 |
即AD=CD×
| ||
| 3 |
在Rt△BDC中，∵∠B=45°，
∴∠BCD=45°，
∴CD=BD．
∵AB=DB+DA=CD+CD×
| ||
| 3 |
| 3 |
∴CD=3．
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
9+3
| ||
| 2 |
答：△ABC的面积为=
9+3
| ||
| 2 |
练习册系列答案
相关题目
查，巡逻艇调整好航向，以26海里/小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问：