题目内容
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,若“摸出的球是黑球”为必然事件,求m的值;
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于 ![]() ,求m的值.
,求m的值.
【答案】
(1)解:当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
∴m的值为4
(2)解:根据题意得: ![]() =
= ![]() ,
,
解得:m=2
【解析】(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;(2)利用概率公式列出方程,求得m的值即可.
【考点精析】根据题目的已知条件,利用概率公式的相关知识可以得到问题的答案,需要掌握一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.

 步步高达标卷系列答案
步步高达标卷系列答案【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙两个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙两个小组各项得分如下表:
小组 | 研究报告 | 小组展示 | 答辩 |
甲 | 91 | 80 | 78 |
乙 | 79 | 83 | 90 |
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果研究报告、小组展示、答辩按照4:3:3计算成绩,哪个小组的成绩最高?
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF= ![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G. 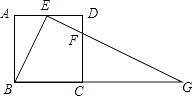
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.