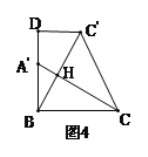题目内容
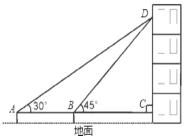
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A.B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度
(计算结果精确到0.1米,参考数据
≈1.414,
≈1.732)
【答案】15.1m
【解析】
首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形Rt△BCD、Rt△ACD,应利用其公共边DC构造方程关系式,进而可解即可求出答案
在Rt△BCD中,tan45°=
,∴CD=BC.
在R△ACD中,tan30°=
AC
∴
∴
∴3CD=
∴
≈13.66(米)
∴条幅顶端D点距离地面的高度为13.66+1.4=15.1(米)
练习册系列答案
相关题目
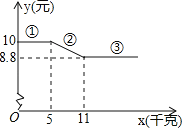
【题目】环保局对某企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0 mg/L．环保局要求该企业立即整改，在15天以内（含15天）排污达标．整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，其中第3天时硫化物的浓度降为4 mg/L．从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系：
时间x（天） | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y（mg/L） | 4 | 3 | 2.4 | 2 | 1.5 |
（1）求整改过程中当0≤x<3时，硫化物的浓度y与时间x的函数表达式；
（2）求整改过程中当x≥3时，硫化物的浓度y与时间x的函数表达式；
（3）该企业所排污水中硫化物的浓度，能否在15天以内不超过最高允许的1.0 mg/L？为什么？
