题目内容
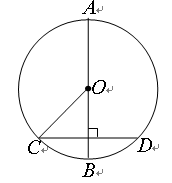
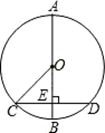
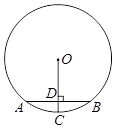
如图,AB是⊙O直径,且AB=4cm,弦CD⊥AB,∠COB=45°,则CD为 ▲ cm.

2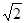
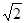
根据已知条件求得圆的半径OC=2;然后由垂径定理知CE=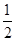 CD;再在直角三角形OEC中利用勾股定理求得CE的值.
CD;再在直角三角形OEC中利用勾股定理求得CE的值.
解:∵AB是⊙O直径,AB=4cm,
∴OC=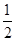 AB=2(半径是直径的一半);
AB=2(半径是直径的一半);
∵AB是⊙O直径,CD⊥AB,
∴CE=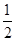 CD(垂径定理);
CD(垂径定理);
又∵∠COB=45°,
∴∠OCB=45°,
∴∠COB=∠OCB=45°,
∴OE=CE(等角对等边);
在直角三角形OCE中,OC2=OE2+CE2,
∴CE=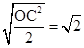 ,
,
∴CD=2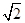 .
.
故答案为:2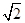 .
.
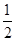 CD;再在直角三角形OEC中利用勾股定理求得CE的值.
CD;再在直角三角形OEC中利用勾股定理求得CE的值.解:∵AB是⊙O直径,AB=4cm,

∴OC=
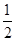 AB=2(半径是直径的一半);
AB=2(半径是直径的一半);∵AB是⊙O直径,CD⊥AB,
∴CE=
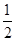 CD(垂径定理);
CD(垂径定理);又∵∠COB=45°,
∴∠OCB=45°,
∴∠COB=∠OCB=45°,
∴OE=CE(等角对等边);
在直角三角形OCE中,OC2=OE2+CE2,
∴CE=
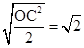 ,
,∴CD=2
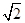 .
.故答案为:2
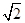 .
.
练习册系列答案
相关题目
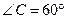 ,
,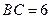 ,B点坐标为(4,0).点
,B点坐标为(4,0).点 是边
是边 上一点,且
上一点,且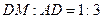 .点
.点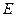 、
、 分别从
分别从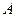 、
、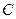 同时出发,以1厘米/秒的速度分别沿
同时出发,以1厘米/秒的速度分别沿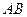 、
、 向点
向点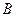 运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为
运动(当点F运动到点B时,点E随之停止运动),EM、CD的延长线交于点P,FP交AD于点Q.⊙E半径为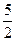 ,设运动时间为
,设运动时间为 秒。
秒。
 ?
?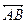 的中点,CD是⊙O的直径,过C点的直线
的中点,CD是⊙O的直径,过C点的直线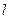 交AB所在直线于点E,交⊙O于点F。
交AB所在直线于点E,交⊙O于点F。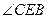 与
与 的数量关系,并写出结论;
的数量关系,并写出结论;

 ,OB长为半径作圆,恰好经过点A,并与BC交于点D.
,OB长为半径作圆,恰好经过点A,并与BC交于点D. ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).


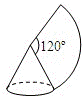
 ,内切圆半径是
,内切圆半径是 ,则内切圆的面积与三角形面积之比是( )
,则内切圆的面积与三角形面积之比是( )


