题目内容
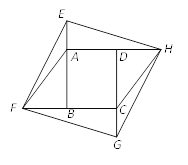
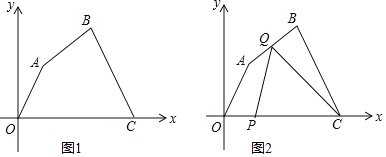
【题目】如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别为O(0,0),A(3,3![]() )、B(9,5
)、B(9,5![]() ),C(14,0),动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA﹣AB﹣BC运动,在OA、AB、BC上运动的速度分别为3,
),C(14,0),动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA﹣AB﹣BC运动,在OA、AB、BC上运动的速度分别为3,![]() ,
,![]() (单位长度/秒),当P、Q中的一点到达C点时,两点同时停止运动.
(单位长度/秒),当P、Q中的一点到达C点时,两点同时停止运动.
(1)求AB所在直线的函数表达式;
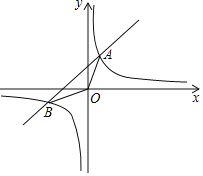
(2)如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值;
(3)在P、Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.
【答案】(1)![]() ;(2)S=
;(2)S=![]() (2≤t≤6),当t=5时,S有最大值为
(2≤t≤6),当t=5时,S有最大值为![]() ;(3)t的值为
;(3)t的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
试题(1)利用待定系数法求AB所在直线的函数表达式;
(2)由题意得:OP=t,PC=14﹣t,求出PC边上的高,代入面积公式计算,并根据二次函数的最值公式求出最大值即可;
(3)分别以Q在OA、AB、BC上运动时讨论:
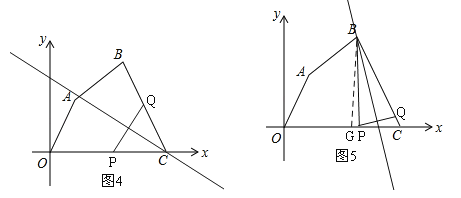
①当0<t≤2时,线段PQ的中垂线经过点C(如图2),②当2<t≤6时,线段PQ的中垂线经过点A(如图3),③当6<t≤10时,i)线段PQ的中垂线经过点C(如图4),ii)线段PQ的中垂线经过点B(如图5),只要能画出图形,根据中垂线的性质和勾股定理列方程可得结论.
试题解析:(1)设AB所在直线的函数表达式为y=kx+b,把A(3,![]() )、B(9,
)、B(9,![]() )代入得:
)代入得: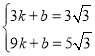 ,解得:
,解得: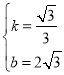 ,∴AB所在直线的函数表达式为
,∴AB所在直线的函数表达式为![]() ;
;
(2)如图1,由题意得:OP=t,则PC=14﹣t,过A作AD⊥x轴于D,过B作BF⊥x轴于F,过Q作QH⊥x轴于H,过A作AE⊥BF于E,交QH于G,∵A(3,![]() ),∴OD=3,AD=
),∴OD=3,AD=![]() ,由勾股定理得:OA=6,∵B(9,
,由勾股定理得:OA=6,∵B(9,![]() ),∴AE=9﹣3=6,BE=
),∴AE=9﹣3=6,BE=![]() ﹣
﹣![]() =
=![]() ,Rt△AEB中,AB=
,Rt△AEB中,AB=![]() =
=![]() ,tan∠BAE=
,tan∠BAE=![]() =
=![]() =
=![]() ,∴∠BAE=30°,点Q过OA的时间:t=6÷3=2(秒),∴AQ=
,∴∠BAE=30°,点Q过OA的时间:t=6÷3=2(秒),∴AQ=![]() (t﹣2),∴QG=
(t﹣2),∴QG=![]() AQ=
AQ=![]() ,∴QH=
,∴QH=![]() +
+![]() =
=![]() ,在△PQC中,PC=14﹣t,PC边上的高为
,在△PQC中,PC=14﹣t,PC边上的高为![]() ,t=
,t=![]() =4(秒),∴S=
=4(秒),∴S=![]() (14﹣t)(
(14﹣t)(![]() ),即S=
),即S=![]() (2≤t≤6),∴当t=5时,S有最大值为
(2≤t≤6),∴当t=5时,S有最大值为![]() ;
;
(3)①当0<t≤2时,线段PQ的中垂线经过点C(如图2),过Q作QG⊥x轴于G,由题意得:OQ=3t,OP=t,∠AOG=60°,∴∠OQG=30°,∴OG=![]() t,∴CG=14﹣
t,∴CG=14﹣![]() t,sin60°=
t,sin60°=![]() ,∴QG=
,∴QG=![]() ×3t=
×3t=![]() ,在Rt△QGC中,由勾股定理得:QG2+CG2=QC2=PC2,可得方程
,在Rt△QGC中,由勾股定理得:QG2+CG2=QC2=PC2,可得方程![]() ,解得:t1=
,解得:t1=![]() ,t2=0(舍),此时t=
,t2=0(舍),此时t=![]() ;
;
②当2<t≤6时,线段PQ的中垂线经过点A(如图3),∴AQ=AP,过A作AG⊥x轴于G,由题意得:OP=t,AQ=![]() (t﹣2),则PG=t﹣3,AP=
(t﹣2),则PG=t﹣3,AP=![]() (t﹣2),在Rt△AGP中,由勾股定理得:AP2=AG2+PG2,可得方程:
(t﹣2),在Rt△AGP中,由勾股定理得:AP2=AG2+PG2,可得方程:![]() ,解得:t1=
,解得:t1=![]() ,t2=
,t2=![]() (舍去),此时t=
(舍去),此时t=![]() ;
;
③当6<t≤10时,分两种情况:
i)线段PQ的中垂线经过点C(如图4),∴PC=CQ,由(2)知:OA=6,AB=![]() ,BC=10,t=
,BC=10,t=![]() =6,∴BQ=
=6,∴BQ=![]() (t﹣6),∴CQ=BC﹣BQ=10﹣
(t﹣6),∴CQ=BC﹣BQ=10﹣![]() (t﹣6)=25﹣
(t﹣6)=25﹣![]() t,可得方程为:14﹣t=25﹣
t,可得方程为:14﹣t=25﹣![]() t,解得:t=
t,解得:t=![]() ;
;
ii)线段PQ的中垂线经过点B(如图5),∴BP=BQ,过B作BG⊥x轴于G,则BG=![]() ,PG=t﹣9,BQ=
,PG=t﹣9,BQ=![]() (t﹣6),由勾股定理得:BP2=BG2+PG2,可得方程为:
(t﹣6),由勾股定理得:BP2=BG2+PG2,可得方程为:![]() ,解得:t1=
,解得:t1=![]() ,t2=
,t2=![]() (舍去),此时t=
(舍去),此时t=![]() ,综上所述,t的值为
,综上所述,t的值为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
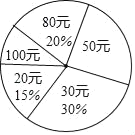
小学生10分钟应用题系列答案【题目】在“全民读书月”活动中,小明调查了班级里40名同学本学期购买课外书的费用情况,并将结果绘制成如图所示的统计表和扇形统计图,请根据相关信息,解答下列问题:(直接填写结果)
费用(元) | 20 | 30 | 50 | 80 | 100 |
人数 | 6 | a | 10 | b | 4 |
(1)本次调查获取的样本数据的众数是 元,中位数是 元;
(2)扇形统计图中,“50元”所对应的圆心角的度数为 度,该班学生购买课外书的平均费用为 元;
(3)若该校共有学生1000人,根据样本数据,估计本学期购买课外书花费50元的学生有 人.