题目内容
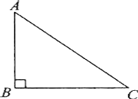
【题目】如图,△ABC中,∠B=90°,AB=3,BC=4,AC=5;
实践与操作:过点A作一条直线,使这条直线将△ABC分成面积相等的两部分,直线与BC交于点D.(尺规作图,不写作法,保留作图痕迹,标清字母)
推理与计算:求点D到AC的距离.
【答案】作图见解析,点D到AC的距离为:![]()
【解析】
根据三角形的面积公式,只需过点A和BC的中点D画直线即可;作DH⊥AC,证得△CHD∽△CBA,利用对应边成比例求得答案.
作线段BC的垂直平分线EF交BC于D,过A、D画直线,则直线AD为所求
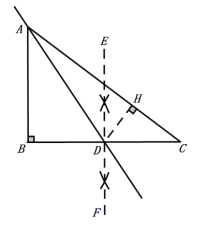
作DH⊥AC于H.
∵∠C=∠C,∠CHD=∠B=90°,
∴△CHD∽△CBA,
∴![]() ,
,
∵BD=DC=2,AB=3,AC=5,
∴![]() ,
,
∴![]()
∴点D到AC的距离为:![]()

练习册系列答案
相关题目
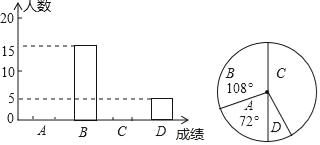
【题目】某校九年级数学测试后,为了解学生学习情况,随机抽取了九年级部分学生的数学成绩进行统计,得到相关的统计图表如下.
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的数学成绩,补全频数分布直方图;
(2)若该校九年级有1000名学生,请据此估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有多少人?
(3)根据学习中存在的问题,通过一段时间的针对性复习与训练,若A等级学生数可提高40%,B等级学生数可提高10%,请估计经过训练后九年级数学成绩在B等级以上(含B等级)的学生可达多少人?