题目内容
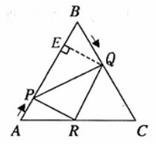
如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：
（1）当t＝2时，判断△BPQ的形状，并说明理由；
（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；
（3）作QR//BA交AC于点R，连结PR，当t为何值时，△APR∽△PRQ？
解：（1）
是等边三角形．
当
时．
．
．
．
又
，
是等边三角形．
（2）过
作
，垂足为
．
由
，得
．
由
，得
．
．(
（3）
，
．
又
，
是等边三角形．
．
，
，
．
四边形
是平行四边形．
．
又
，
．
，
．
，即
．
解得
．
当时，
．
练习册系列答案
名校课堂系列答案
相关题目
的坐标为（-1，0）．
如图，已知△ABC是等边三角形，AB交⊙O于点D，DE⊥AC于点E．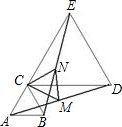
如图，已知△ABC是等边三角形，E是AC延长线上一点，选择一点D，使得△CDE是等边三角形，如果M是线段AD的中点，N是线段BE的中点，
（2012•襄城区模拟）如图，已知△ABC是等边三角形，D、E分别在边BC、AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF、BE和CF．
（2013•奉贤区二模）如图，已知△ABC是等边三角形，点D是BC延长线上的一个动点，以AD为边作等边△ADE，过点E作BC的平行线，分别交AB，AC的延长线于点F，G，联结BE．