题目内容
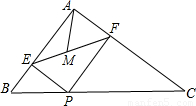
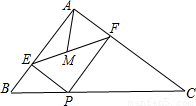
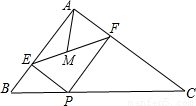
 (2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
(2012•襄城区模拟)如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.(1)求证:△BCE≌△FDC;
(2)判断四边形ABDF是怎样的四边形,并说明理由.
分析:(1)根据已知条件可以判定△ABC、△DCE均为等边三角形,由等边三角形的三个内角相等、三条边相等,利用全等三角形的判定定理SAS可以证得结论;
(2)四边形ABDF是平行四边形;利用(1)中的三个等边三角形△ABC、△AEF、△DCE可以推知同位角∠CDE=∠ABC,内错角∠CDE=∠EFA.所以利用平行的线的判定定理可以证得四边形ABDF的对边相互平行.
(2)四边形ABDF是平行四边形;利用(1)中的三个等边三角形△ABC、△AEF、△DCE可以推知同位角∠CDE=∠ABC,内错角∠CDE=∠EFA.所以利用平行的线的判定定理可以证得四边形ABDF的对边相互平行.
解答: (1)证明:∵△ABC是等边三角形,
(1)证明:∵△ABC是等边三角形,
∴AC=BC=AB,∠ACB=60°;
又∵CD=CE,
∴△EDC是等边三角形,
∴DE=CD=CE,∠DCE=∠EDC=60°,
∵EF=AE,
∴EF+DE=AE+CE,
∴FD=AC=BC,
∴△BCE≌△FDC(SAS);
(2)解:四边形ABDF是平行四边形;
理由如下:
∵由(1)知△ABC、△AEF、△DCE均为等边三角形,
∴∠CDE=∠ABC=∠EFA=60°,
∴AB∥FD,BD∥AF,
∴四边形ABDF是平行四边形.
 (1)证明:∵△ABC是等边三角形,
(1)证明:∵△ABC是等边三角形,∴AC=BC=AB,∠ACB=60°;
又∵CD=CE,
∴△EDC是等边三角形,
∴DE=CD=CE,∠DCE=∠EDC=60°,
∵EF=AE,
∴EF+DE=AE+CE,
∴FD=AC=BC,
∴△BCE≌△FDC(SAS);
(2)解:四边形ABDF是平行四边形;
理由如下:
∵由(1)知△ABC、△AEF、△DCE均为等边三角形,
∴∠CDE=∠ABC=∠EFA=60°,
∴AB∥FD,BD∥AF,
∴四边形ABDF是平行四边形.
点评:本题考查了全等三角形的判定与性质、等边三角形的性质以及平行四边形的判定.平行四边形的判定定理:①对边平行且相等的四边形是平行四边形;②两组对边相互平行的四边形是平行四边形;③对角线互相平分的四边形是平行四边形.

练习册系列答案
相关题目