Question

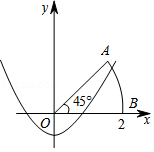
【题目】如图，在平面直角坐标系中，点O为坐标原点，点在第一象限，过点A向x轴作垂线，垂足为点B，连接OA，，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点B出发以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，连接AM，AN，MN．

求a的值；

当时，

请探究，，之间的数量关系，并说明理由；

试判断四边形AMON的面积是否变化？若不变化，请求出其值；若变化，请说明理由．

当时，请求出t的值．

Answer 1

【答案】（1）a=2（2）①∠ANM=∠OMN+∠BAN②详见解析（3）t=或6

【解析】

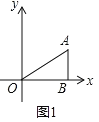
（2）当0＜t＜2时①∠ANM=∠OMN+∠BAN．如图2中，过N点作NH∥AB，利用平行的性质证明即可．②根据S四边形AMON =S四边形ABOM-S三角形ABN，计算即可；

（3）分两种情形列出方程即可解决问题；

∵S三角形AOB=12，A（3a，2a），

∴×3a×2a=12，

∴=4，

又∵a＞0，

∴a=2．

（2）当0＜t＜2时,

①∠ANM=∠OMN+∠BAN，

如图2中，过N点作NH∥AB，

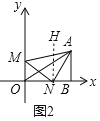
∵AB⊥X轴,

∴AB∥OM,

∴AB∥NH∥OM,

∴∠OMN=∠MNH,

∠BAN=∠ANH,

∴∠ANM=∠MNH+∠ANH,

=∠OMN+∠BAN．

②S四边形AMON 不变化,

理由：∵a=2,

∴A（6，4）,

∴OB=6，AB=4，OM=2t BN=3t,

ON=6-3t,

∴S四边形AMON =S四边形ABOM-S三角形ABN，

=（AB+OM）×OB-×BN×AB

=（4+2t）×6-×3t×4

=12+6t-6t

=12

∴四边形AMON的面积不变,

（3）t=或6．