题目内容
在平面直角坐标系xOy中,有一抛物线y=x2-2x-3,与x轴交于点B、点C (B在C的左侧),点A在该抛物线上,且横坐标为-2,蓬接AB、AC现将背面完全相同,正面分别标有数-2、-1、0、1、2的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数加1作为点P的纵坐标,则点P落在△ABC内(含边界)的概率为分析:首先由抛物线y=x2-2x-3,与x轴交于点B、点C (B在C的左侧),点A在该抛物线上,且横坐标为-2,根据点与二次函数的关系,即可求得点A,B,C的坐标,然后利用待定系数法求得直线AB与AC的解析式;又由题意求得点P的所有可能的情况与点P落在△ABC内(含边界)情况,利用概率公式即可求得答案.
解答:解:∵当x2-2x-3=0时,
解得:x1=3,x2=-1,
∵抛物线y=x2-2x-3,与x轴交于点B、点C (B在C的左侧),
∴点B的坐标为(-1,0),点C的坐标为(3,0),
∵点A在该抛物线上,且横坐标为-2,
∴y=4-2×(-2)-3=5,
∴点A的坐标为(-2,5),
∴设直线AB的解析式为:y=kx+b,
则
,
解得:
,
∴直线AB的解析式为:y=-5x-5,
同理可得,直线AC的解析式为:y=-x+3,
根据题意得:点P的坐标的所有可能为:(-2,-1),(-1,0),(0,1),(1,2),(2,3),
∴点P落在△ABC内(含边界)的有((-1,0),(0,1),(1,2),
∴点P落在△ABC内(含边界)的概率为:
.
故答案为:
.
解得:x1=3,x2=-1,
∵抛物线y=x2-2x-3,与x轴交于点B、点C (B在C的左侧),
∴点B的坐标为(-1,0),点C的坐标为(3,0),
∵点A在该抛物线上,且横坐标为-2,
∴y=4-2×(-2)-3=5,
∴点A的坐标为(-2,5),
∴设直线AB的解析式为:y=kx+b,
则
|
解得:
|
∴直线AB的解析式为:y=-5x-5,
同理可得,直线AC的解析式为:y=-x+3,
根据题意得:点P的坐标的所有可能为:(-2,-1),(-1,0),(0,1),(1,2),(2,3),
∴点P落在△ABC内(含边界)的有((-1,0),(0,1),(1,2),
∴点P落在△ABC内(含边界)的概率为:
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:此题考查了点与二次函数的关系,待定系数法求一次函数的解析式以及概率的知识.此题综合性较强,难度较大,解题的关键是注意方程思想的应用,注意熟记概率公式.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
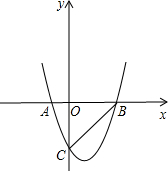 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为