题目内容
在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c的对称轴是x=1,并且经过(-2,-5)和(5,-12)两点.(1)求此抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C 点,D是线段BC上一点(不与点B、C重合),若以B、O、D为顶点的三角形与△BAC相似,求点D的坐标;
(3)点P在y轴上,点M在此抛物线上,若要使以点P、M、A、B为顶点的四边形是平行四边形,请你直接写出点M的坐标.
分析:(1)根据待定系数法列出方程组,求出a、b、c的值即可;
(2)根据抛物线解析式求出与x轴、y轴的交点,根据相似三角形的性质列出比例式,结合勾股定理解答即可;
(3)画出图形,根据平行四边形的性质即可得到M点的坐标.
(2)根据抛物线解析式求出与x轴、y轴的交点,根据相似三角形的性质列出比例式,结合勾股定理解答即可;
(3)画出图形,根据平行四边形的性质即可得到M点的坐标.
解答: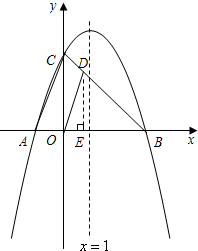 解:(1)由题意,得
解:(1)由题意,得
,
解这个方程组,得
,(1分)
∴抛物线的解析式为y=-x2+2x+3.(2分)
(2)令y=0,得-x2+2x+3=0.
解这个方程,得x1=-1,x2=3.
∴A(-1,0),B(3,0).
令x=0,得y=3.
∴C(0,3).
∴AB=4,OB=OC=3,∠OBC=45°.
∴BC=
=
=3
.
过点D作DE⊥x轴于点E.
∵∠OBC=45°,
∴BE=DE.
要使△BOD∽△BAC或△BDO∽△BAC,
已有∠ABC=∠OBD,则只需
=
或
=
成立.
若
=
成立,
则有BD=
=
=
.
在Rt△BDE中,由勾股定理,得BE2+DE2=2BE2=BD2=(
)2.
∴BE=DE=
.
∴OE=OB-BE=3-
=
.
∴点D的坐标为(
,
).(4分)
若
=
成立,则有BD=
=
=2
.
在Rt△BDE中,由勾股定理,得BE2+DE2=2BE2=BD2=(2
)2.
∴BE=DE=2.
∴OE=OB-BE=3-2=1.
∴点D的坐标为(1,2).(5分)
∴点D的坐标为(
,
)或(1,2);
(3)点M的坐标为(2,3)或(4,-5)或(-4,-21).(8分)
 解:(1)由题意,得
解:(1)由题意,得
|
解这个方程组,得
|
∴抛物线的解析式为y=-x2+2x+3.(2分)
(2)令y=0,得-x2+2x+3=0.
解这个方程,得x1=-1,x2=3.
∴A(-1,0),B(3,0).
令x=0,得y=3.
∴C(0,3).
∴AB=4,OB=OC=3,∠OBC=45°.
∴BC=
| OB2+OC2 |
| 32+32 |
| 2 |
过点D作DE⊥x轴于点E.
∵∠OBC=45°,
∴BE=DE.
要使△BOD∽△BAC或△BDO∽△BAC,
已有∠ABC=∠OBD,则只需
| BD |
| BC |
| BO |
| BA |
| BO |
| BC |
| BD |
| BA |
若
| BD |
| BC |
| BO |
| BA |
则有BD=
| BO×BC |
| BA |
3×3
| ||
| 4 |
9
| ||
| 4 |
在Rt△BDE中,由勾股定理,得BE2+DE2=2BE2=BD2=(
9
| ||
| 4 |
∴BE=DE=
| 9 |
| 4 |
∴OE=OB-BE=3-
| 9 |
| 4 |
| 3 |
| 4 |
∴点D的坐标为(
| 3 |
| 4 |
| 9 |
| 4 |
若
| BO |
| BC |
| BD |
| BA |
| BO×BA |
| BC |
| 3×4 | ||
3
|
| 2 |
在Rt△BDE中,由勾股定理,得BE2+DE2=2BE2=BD2=(2
| 2 |
∴BE=DE=2.
∴OE=OB-BE=3-2=1.
∴点D的坐标为(1,2).(5分)
∴点D的坐标为(
| 3 |
| 4 |
| 9 |
| 4 |
(3)点M的坐标为(2,3)或(4,-5)或(-4,-21).(8分)
点评:本题主要考查了待定系数法求二次函数解析式、函数图象与x轴、y轴交点的求法等知识点.主要考查学生数形结合的数学思想方法,画出相关图形,是解题必不可少的环节.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为