Question

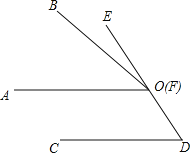
【题目】如图，下列条件中不能判定AB∥CD的是（　　）

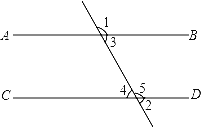
A. ∠3=∠4 B. ∠1=∠5 C. ∠4+∠5=180° D. ∠3+∠5=180°

Answer 1

【答案】C

【解析】

根据同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行;可以进行判定.

A选项,因为∠3和∠4一组内错角,且∠3=∠4,根据内错角相等两直线平行可以判定AB∥CD,不符合题意,

B选项,因为∠1和∠5 是一组同位角,且∠1=∠5根据同位角相等两直线平行可以判定AB∥CD,不符合题意,

C选项,因为∠4和∠5一组邻补角,所以∠4+∠5=180°不能判定两直线平行,

D选项,因为∠3和∠5是一组同旁内角,且∠3+∠5=180°,根据根据同旁内角互补两直线平行可以判定AB∥CD,不符合题意,

故选C.