题目内容
【题目】如图，等边△ABC的边长是2，D,E分别为AB，AC的中点，延长BC至点F，使CF＝
BC连接CD和EF.
（1）求证：DE=CF；
（2）求EF的长.
【答案】（1）见解析；（2）
【解析】试题分析：（1）直接利用三角形中位线定理得出DE=
BC，进而得出DE=FC；
（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长即可.
试题解析：（1）∵D、E分别为AB、AC的中点，∴DE=BC，
∵CF=BC， ∴DE=FC；
（2）∵D、E分别为AB、AC的中点，
∴DE是△ABC的中位线，∴DE//BC，即DE//CF，
又∵DE=CF，∴四边形DEFC是平行四边形，∴DC=EF，
∵D为AB的中点，等边△ABC的边长是2，∴AD=BD=1，CD⊥AB，BC=2，
∴DC=，
∴EF=.
练习册系列答案
轻松暑假总复习系列答案
相关题目
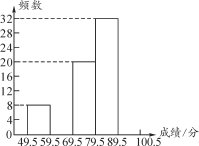
【题目】6月5日是世界环境日，为了普及环保知识，增强环保意识，某市第一中学举行了“环保知识竞赛”，参赛人数为1 000人．为了了解本次竞赛的成绩情况，学校团委从中抽取部分学生的成绩(满分为100分，最少为50分，得分取整数)进行统计，并绘制出不完整的频数分布表和不完整的频数分布直方图如下：
分组 | 频数 | 所占百分比 |
49.5～59.5 | 8 | 8% |
59.5～69.5 | __ __ | 12% |
69.5～79.5 | 20 | __ __ |
79.5～89.5 | 32 | __ __ |
89.5～100.5 | __ __ | 28% |
(1)补全频数分布表和频数分布直方图；
(2)若成绩在80分以上为优秀，求这次参赛的学生中成绩为优秀的约有多少人．
