Question

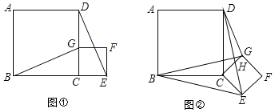
【题目】如图，在边长为8的等边△ABC中，点D是AB的中点，点E是平面上一点，且线段DE=2，将线段EB绕点E顺时针旋转60得到线段EF，连接AF.

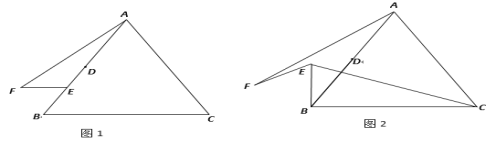
（1）如图1，当BE=2时，求线段AF的长；

（2）如图2，求证：AF=CE；

Answer 1

【答案】（1） （2）见解析

【解析】

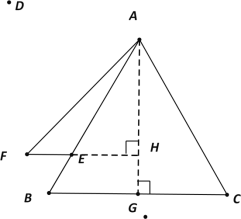
(1)作AG⊥BC于G点，延长FE交AG于H点,构造有60角的直角三角形，再运用勾股定理可求解；

(2)利用等边三角形的性质可证明△FBA≌△EBC，从而证明AF=CE.

解：(1)作AG⊥BC于G点，延长FE交AG于H点

∵AB=AC，

∴∠BAG=30，

∵EB绕点E顺时针旋转60得到线段EF，

∴∠BEF=60，

∴∠BEF=∠B，

∴EF∥BC，

∵AG⊥BC，

∴AG⊥FH，

在Rt△AEH中,∵AE=6,∠EAH=30，

∴,，

在Rt△AFH中，.

(2)连接FB，

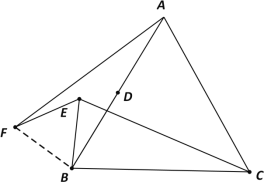
∵EB绕点E顺时针旋转60得到线段EF，

∴△EBF是等边三角形，

∴FB=EB, ∴∠FBE=∠ABC=60

∴∠FBE+∠EBA=∠ABC+∠EBA

即∠FBA=∠EBC，

又∵AB=BC，

∴△FBA≌△EBC ，

∴AF=CE，