Question

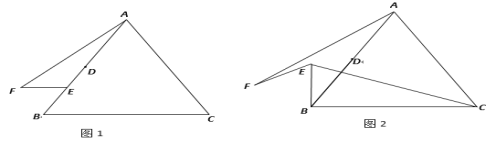
【题目】如图①，B，C，E是同一直线上的三个点， 四边形ABCD与四边形CEFG都是正方形．连接BG，DE.

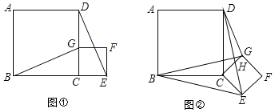
(1)探究BG与DE之间的数量关系， 并证明你的结论；

(2)当正方形CEFG绕点C在平面内顺时针转动到如图②所示的位置时，线段BG和ED有何关系? 写出结论并证明.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）猜想BG⊥BD，且BG=DE，延长BG与DE交于H点，用SAS证明△BCG≌△DCE，得出BG=DE，∠CBG=∠CDE，再证明∠DHG=90°，即可得出结论；

（2）用SAS证明△BCG≌△DCE，得出BG=DE，∠CBG=∠CDE，再根据对顶角相等和直角三角形两锐角互余，通过等量代换即可得出结论．

（1）猜想：BG⊥BD，且BG=DE．证明如下：

延长BG与DE交于H点．

∵ABCD和CEFG都是正方形，

∴BC=DC，GC=EC，∠BCG=∠DCE=90°．

在△BCG和△DCE中，∵BC=DC，∠BCG=∠DCE=90°，GC=EC，

∴△BCG≌△DCE，

∴∠BGC=∠DEC，BG=DE．

又∵∠BGC=∠DGH，∠DEC+∠CDE=90°，

∴∠DGH+∠GDH=90°，

∴∠DHG=90°，

故BG⊥DE，且BG=DE．

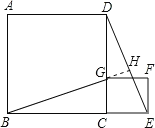
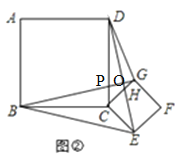
（2）BG=DE，BG⊥DE．证明如下：

∵四边形ABCD、CEFG都是正方形，

∴BC=CD，CG=CE，∠BCD=∠ECG，

∴∠BCG=∠DCE，

∴△BCG≌△DCE（SAS），

∴BG=DE，∠CBG=∠CDE．

又∵∠BPC=∠DPO，∠CBG+∠BPC=90°，

∴∠CDE+∠DPO=90°，

∴∠DOP=90°，

∴BG⊥DE，

∴BG=DE，BG⊥DE．