题目内容
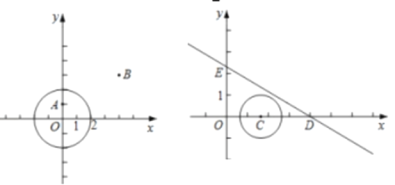
【题目】如图1,矩形![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为(2,0),(0,3) ,抛物线
的坐标分别为(2,0),(0,3) ,抛物线![]() :
:![]() 经过
经过![]() ,
,![]() 两点.抛物线的顶点为
两点.抛物线的顶点为![]() .
.

(1)求抛物线![]() 的表达式和点
的表达式和点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线
是抛物线![]() 对称轴上一动点,当
对称轴上一动点,当![]() 为等腰三角形时,求所有符合条件的点
为等腰三角形时,求所有符合条件的点![]() 的坐标;
的坐标;
(3)如图2,现将抛物线![]() 进行平移,保持顶点在直线
进行平移,保持顶点在直线![]() 上,若平移后的抛物线与射线
上,若平移后的抛物线与射线![]() 只有一个公共点.设平移后抛物线的顶点横坐标为
只有一个公共点.设平移后抛物线的顶点横坐标为![]() ,求
,求![]() 的值或取值范围.
的值或取值范围.
【答案】(1)(1,4);(2)![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)由题意可知B,C两点的坐标,利用待定系数法即可解决问题;
(2)分三种不同的情况:①当AC=AP时,②当AC=CP时,③当AP=CP时,设P(1,t),根据两点间的距离公式,求出AC2=9+4=13,AP2=1+t2,CP2=1+(t-3)2,分别列出方程即可解决;
(3)先求得直线CD的解析式,利用直线与抛物线的交点、抛物线的平移变换规律来求m的取值范围即可.
(1)∵矩形![]() 的顶点
的顶点![]() ,
,![]() 的坐标分别为(2,0),(0,3)
的坐标分别为(2,0),(0,3)
∴OA=2,OC=3,即B(2,3)
把点![]() 、
、![]() 分别代入
分别代入![]() ,得
,得
![]()
解得![]() ,
,
则该抛物线的解析式为:![]() ;
;
又∵![]()
∴顶点![]()
(2)设![]() ,
,
![]() ,
,![]() ,
,![]()
①当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() 或
或![]()
②当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() 或
或![]()
③当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]()
(3)∵![]() 、
、![]() ,
,
∴易得直线![]() 的解析式为:
的解析式为:![]() ,移动中抛物线的顶点为
,移动中抛物线的顶点为![]() ,则抛物线为
,则抛物线为![]() ,
,
又![]() ,
,![]() ,
,
将![]() 代入,
代入,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]()
又![]()
∴![]() ,
,
∵![]() ,
,
解得![]()
∴顶点横坐标![]() 的值或取值范围为
的值或取值范围为![]() 或
或![]() .
.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请求出y与x之间的函数关系式.
(2)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
(3)如果每天获得不低于160元的利润,销售单价范围是多少?至少出售多少袋?
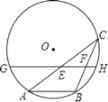
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为8,则GE+FH的最大值为__________ .
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?