题目内容
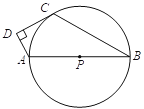
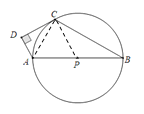
【题目】如图,已知AB是⊙P的直径,点![]() 在⊙P上,
在⊙P上,![]() 为⊙P外一点,且∠ADC=90°,直线
为⊙P外一点,且∠ADC=90°,直线![]() 为⊙P的切线.
为⊙P的切线.
⑴ 试说明:2∠B+∠DAB=180°
⑵ 若∠B=30°,AD=2,求⊙P的半径.
【答案】(1)证明见解析;(2)4.
【解析】
(1)根据切线的性质和圆周角定理,以及平行线的性质即可得到结论;
(2)连接AC,易证△ACP是等边三角形,得到∠ACD=30°即可求出半径.
解:⑴ 连接CP
∵PC=PB,∴∠B=∠PCB,
∴∠APC=∠PCB+∠B=2∠B
∵CD是⊙OP的切线,∴∠DCP=90°
∵∠ADC=90°,∴∠DAB+∠APC=180°
∴2∠B+∠DAB=180°
⑵ 连接AC
∵∠B=30°,∴∠APC=60°,
∵PC=PA,∴△ACP是等边三角形,∴AC=PA,∠ACP=60°
∴∠ACD=30°,∴AC=2AD=4,∴PA=4
答:⊙P的半径为4.

练习册系列答案
相关题目