Question

【题目】如图，四边形ABCD内接于⊙O，若∠B=130°，OA=1，则 的长为 ．

Answer 1

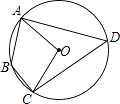
【答案】
【解析】解：∵四边形ABCD内接于⊙O，∠B=130°，

∴∠D=50°，

由圆周角定理得，∠AOC=2∠D=100°，

则 的长= = ，

所以答案是： ．

【考点精析】本题主要考查了圆周角定理和圆内接四边形的性质的相关知识点，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形才能正确解答此题．