题目内容
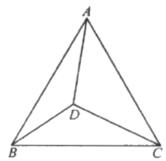
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,射线
,射线![]() 从与射线
从与射线![]() 重合的位置开始,绕点
重合的位置开始,绕点![]() 按顺时针方向旋转,与射线
按顺时针方向旋转,与射线![]() 重合时就停止旋转,射线
重合时就停止旋转,射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
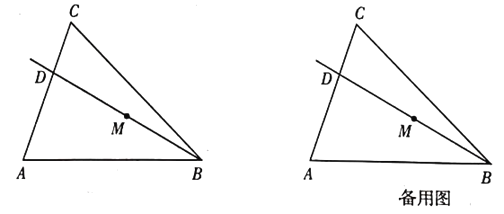
(1)求线段![]() 的长;
的长;
(2)①当点![]() 与点
与点![]() 、点
、点![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,在射线
,在射线![]() 旋转的过程中,
旋转的过程中,![]() 的大小是否发生变化?若不变,求
的大小是否发生变化?若不变,求![]() 的度数;若变化,请说明理由.
的度数;若变化,请说明理由.
②在①的条件下,连接![]() ,直接写出
,直接写出![]() 面积的最小值____________.
面积的最小值____________.
【答案】(1)![]() ;(2)不变,∠EMF=90°,理由见解析;(3)
;(2)不变,∠EMF=90°,理由见解析;(3)![]()
【解析】
(1)如下图,设AN=x,在Rt△CAN中,利用勾股定理可求得x的值,然后再Rt△CNB中,可求得CB的长;
(2)①如下图,△DEB和△DFB是直角三角形,点M是BD的中点,可得到EM=DM=MB=FM,利用角度转化可得到∠FME=90°;
②可推导出![]() ,则只需要BD最小即可,即BD⊥AC时,△EMF的面积最小.
,则只需要BD最小即可,即BD⊥AC时,△EMF的面积最小.
(1)如下图,过点C作AB的垂线,交AB于点N
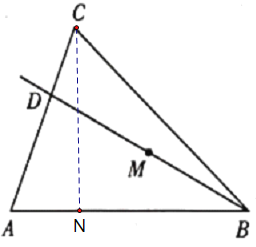
∵![]()
∴设AN=x,则CN=3x
∵![]()
∴在Rt△CAN中,![]()
解得:x=1
∴CN=3,AB=AN+NB=4
∵∠ABC=45°
∴NB=CN=3
∴在Rt△CNB中,CB=3![]() ;
;
(2)①不变,∠EMF=90°
如下图
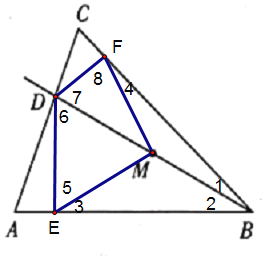
∵DE⊥AB,DF⊥BC
∴△DEB和△DFB是直角三角形
∵点M是DB的中点
∴EM=DM=MB,FM=DM=MB
∴∠2=∠3,∠1=∠4,∠5=∠6,∠7=∠8
∵∠ABC=45°
∴∠1+∠2=45°,∴∠3+∠4=45°
∵∠DEB=∠DFB=90°
∴∠5+∠8=180°-45°=135°
∴∠5+∠6+∠7+∠8=270°
∴在四边形EMFD中,∠EMF=360°-270°=90°;
②如下图
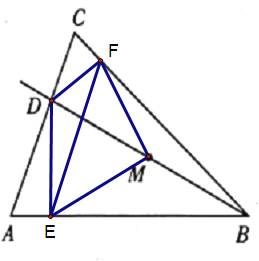
∵∠EFM=0°,EM=FM=DM=MB
∴![]()
要使![]() 最小,则只需要BD最小即可
最小,则只需要BD最小即可
故BD⊥AC,图形如下
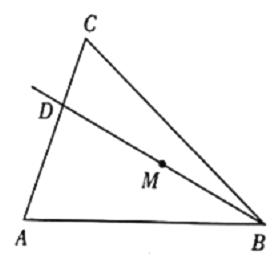
∵![]()
∴设AD=y,则DB=3y
∵AB=4
∴在Rt△ADB中,![]()
解得:y=![]()
∴BD=3y=![]()
∴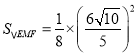 =
=![]() .
.