题目内容
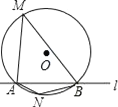
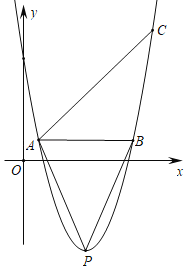
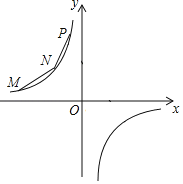
【题目】如图所示,M、N、P在第二象限,横坐标分别是﹣4、﹣2、﹣1,双曲线y=![]() 过M、N、P三点,且MN=NP.
过M、N、P三点,且MN=NP.
(1)求双曲线的解析式;
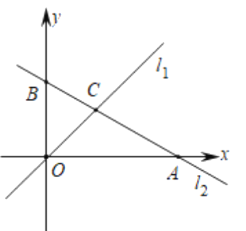
(2)过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y=![]() 于另一点Q,求Q点坐标;
于另一点Q,求Q点坐标;
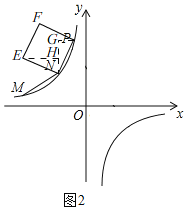
(3)以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落在反比例函数y=![]() 上,求F对应点F′的坐标.
上,求F对应点F′的坐标.
【答案】(1)双曲线的解析式为y=﹣![]() ;(2)Q(
;(2)Q(![]() ,﹣5);(3)点F′的坐标为(﹣5,3).
,﹣5);(3)点F′的坐标为(﹣5,3).
【解析】
(1)先表示出点M,N,P的坐标,进而得出MN2,NP2,建立方程求解,即可得出结论;
(2)分点A在x轴的正半轴或负半轴上,判断出△AOB∽∠PQB,得出比例式,即可得出结论;
(3)先确定出点E,F坐标,设出点N'的坐标,进而得出点E',F',P'的坐标,即可得出结论.
(1)∵双曲线y=![]() 过M、N、P三点,
过M、N、P三点,
∴M(﹣4,﹣![]() ),N(﹣2,﹣
),N(﹣2,﹣![]() ),P(﹣1,﹣k),
),P(﹣1,﹣k),
∴MN2=[(﹣4﹣(﹣2)]2+[(﹣![]() )﹣(﹣
)﹣(﹣![]() )]2=4+
)]2=4+![]() ,NP2=1+
,NP2=1+![]() ,
,
∵MN=NP,
∴MN2=NP2,
∴4+![]() =1+
=1+![]() ,
,
∴k=﹣4或k=4(由于点P在第二象限,不符合题意,舍去),
∴双曲线的解析式为y=﹣![]() ;
;
(2)由(1)知,双曲线的解析式为y=﹣![]() ①,
①,
由(1)知,k=﹣4,
∴P(﹣1,4),
如图1,过点P作PQ⊥y轴于Q,则PQ=1,
Ⅰ、当点A在x轴正半轴时,
∵PA=4AB,
∴PB=3AB,
∵PQ⊥y轴,OA⊥y轴,
∴OA∥PQ,
∴△AOB∽∠PQB,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴OA=![]() ,
,
∴A(![]() ,0),
,0),
∵P(﹣1,4),
∴直线PA的解析式为y=﹣3x+1②,
联立①②解得,![]() 或
或 ,
,
∴Q(![]() ,﹣3),
,﹣3),
Ⅱ、当点A在x轴负半轴上,
∵PA'=A'B',
∴PB'=5A'B',
同(Ⅰ)的方法得,△A'OB'∽△PQB',
∴![]() ,
,
∴![]() ,
,
∴OA'=![]() ,
,
∴A'(﹣![]() ,0),
,0),
∴直线PA'的解析式为y=﹣5x﹣1③,
联立①③解得,![]() 或
或 ,
,
∴Q(![]() ,﹣5);
,﹣5);
(3)如图2,由(1)知,k=﹣4,
∴P(﹣1,4),N(﹣2,2),
∵四边形PNEF是正方形,
∴EN=PN,∠PNE=90°,
过点N作y轴的平行线交过点P作x轴的平行线于G,过点E作EH⊥NG于H,
∴∠EHN=∠NGP=90°,
∴∠HEN+∠ENH=90°,∠ENH+∠PNG=90°,
∴∠HEN=∠GNP,
∴△EHN≌△NGP(AAS),
∴NH=PG=|﹣2﹣(﹣1)|=1,EH=NG=|4﹣2|=2,
∴E(﹣4,3),
同理:F(﹣3,5),
记点N平移到x轴的N'位置,设N'(m,0),
∵N(﹣1,4),
∴点N向左平移(﹣2﹣m)个单位,再向下平移2个单位,
∴点P,E,F也向左平移(﹣2﹣m)个单位,再向下平移2个单位,得到点P'(m+1,2),E'(m﹣2,1),F'(m﹣1,3),
∴点P′、E'正好落在反比例函数y=![]() 上,
上,
∴b=2(m+1)=m﹣2,
∴m=﹣4,
∴F'(﹣5,3),
即F对应点F′的坐标为(﹣5,3).


 活力课时同步练习册系列答案
活力课时同步练习册系列答案