题目内容
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1,0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)求抛物线的函数解析式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
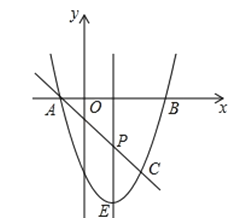
【答案】(1)y=x2﹣2x﹣3;(2)![]() ;(3)F1(1,0),F2(﹣3,0),F3(
;(3)F1(1,0),F2(﹣3,0),F3(![]() ,0),F4(
,0),F4(![]() ,0).
,0).
【解析】
(1)利用待定系数法,直接求出抛物线的解析式即可;
(2)根据点C在抛物线上,求出点C的坐标;根据待定系数法求出直线AC的解析式;设点P的横坐标为x(1≤x≤2),则P、E的坐标分别为P(x,x1),E(x,x22x3),用含x的式子表示出PE的长度,求出PE的最大值;
(3)根据点G的不同位置,分为4种情况讨论,点G在第二象限的抛物线上,点G在抛物线与y轴的交点上(两种情况),点G在直线AC上方y轴右侧,根据平行四边形的对边平行且相等,求得点F的坐标即可.
(1)∵抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0),
∴![]() ,解得:
,解得:![]() ,∴抛物线的函数解析式为:y=x2﹣2x﹣3;
,∴抛物线的函数解析式为:y=x2﹣2x﹣3;
(2)∵点C在抛物线上,且点C的横坐标为2,
∴y=4﹣4﹣3=﹣3,
∴点C的坐标为(2,﹣3),
设直线AC的解析式为:y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为:y=﹣x﹣1,设点P的横坐标为x(﹣1≤x≤2),
则P、E的坐标分别为P(x,﹣x﹣1),E(x,x2﹣2x﹣3).
∵点P在点E的上方,
∴PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2=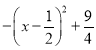 .
.
∵﹣1<0,开口向下,﹣1≤x≤2,
∴当x=![]() 时,PE最大=
时,PE最大=![]() ;
;
(3)存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).
∵A,C,F,G这样的四个点为顶点的四边形是平行四边形
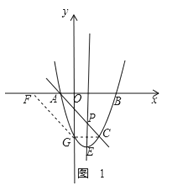
①如图1,四边形AFGC是平行四边形,此时CG∥AF,
∴AF=CG=2,
∴点F的坐标为(﹣3,0);
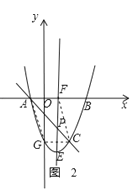
②如图2,四边形AGCF是平行四边形,此时CG∥FA,
∴AF=CG=2.
∵点A的坐标为(﹣1,0),
∴点F的坐标为(1,0);
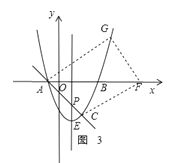
③如图3,四边形ACFG时平行四边形,此时AC∥GF,
此时点C,G两点的纵坐标互为相反数,
故点G的纵坐标为3,且点G在抛物线上,
∴x2﹣2x﹣3=3,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() (舍去),
(舍去),
∴点G的坐标为(1+![]() ,3).
,3).
∵GF∥AC,
∴设直线GF的解析式为:y=﹣x+h,
∴﹣(1+![]() )+h=3,
)+h=3,
解得:h=4+![]() ,
,
∴直线GH的解析式为:y=﹣x+4+![]() ,
,
∴直线GF与x轴的交点F的坐标为(4+![]() ,0);
,0);
④如图4,同③可求得点F的坐标为(4﹣![]() ,0).
,0).
综上所述:存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).

 全能练考卷系列答案
全能练考卷系列答案