Question

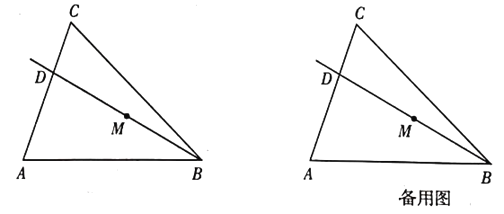
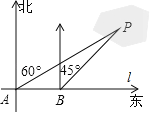
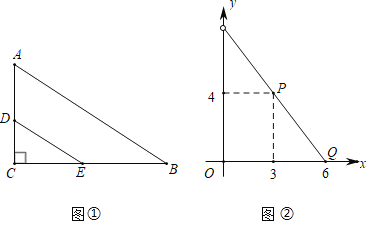
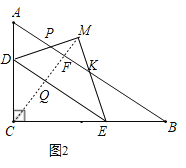
【题目】如图①，在△ABC中，∠C＝90°，AB＝10，BC＝8．点D，E分别是边AC，BC上的动点，连接DE．设CD＝x（x＞0），BE＝y，y与x之间的函数关系如图②所示．

（1）求出图②中线段PQ所在直线的函数表达式；

（2）将△DCE沿DE翻折，得△DME．

①点M是否可以落在△ABC的某条角平分线上？如果可以，求出相应x的值；如果不可以，说明理由；

②直接写出△DME与△ABC重叠部分面积的最大值及相应x的值．

Answer 1

【答案】（1）y＝﹣x+8；（2）①当x＝或x＝时，点M落在△ABC的某条角平分线上；②当x＝4时，△DME与△ABC重叠部分面积的最大值为8．

【解析】

（1）设线段PQ所在直线的函数表达式为y＝kx+b，将P（3，4）和Q（6，0）代入可求得答案；

（2）①连接CM并延长CM交AB于点F，证明△DCE∽△ACB，得出∠DEC＝∠ABC，则DE//AB，求出CF＝，CM＝，MF＝，过点M作MG⊥AC于点M，过点M作MH⊥BC于点H，证得△CGM∽△BCA，则，可得出MG，CG，分三种不同情况可求出答案；

②分两种情形，当0＜x≤3时，当3＜x≤6时，求出△DME与△ABC重叠部分面积的最大值即可．

解：（1）设线段PQ所在直线的函数表达式为y＝kx+b，

将P（3，4）和Q（6，0）代入得，

，解得，

∴线段PQ所在直线的函数表达式为；

（2）①如图1，

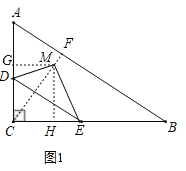
连接CM并延长CM交AB于点F，

∵∠C＝90°，AB＝10，BC＝8，

∴AC＝＝6，

由（1）得BE＝，

∴CE＝，

∴，

∵∠DCE＝∠ACB，

∴△DCE∽△ACB，

∴∠DEC＝∠ABC，

∴DE//AB，

∵点C和点M关于直线DE对称，

∴CM⊥DE，

∴CF⊥AB，

∵，

∴6×8＝10×CF，

∴CF＝,

∵∠C＝90°，CD＝x，CE＝，

∴DE＝，

∴CM＝，MF＝，

过点M作MG⊥AC于点M，过点M作MH⊥BC于点H，

则四边形GCHM为矩形，

∵∠GCM+∠BCF＝∠BCF+∠ABC＝90°，

∴∠GCM＝∠ABC，

∵∠MGC＝∠ACB＝90°，

∴△CGM∽△BCA，

∴，

即，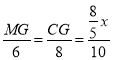

∴MG＝，CG＝，

∴MH＝，

（Ⅰ）若点M落在∠ACB的平分线上，则有MG＝MH，即，解得x＝0（不合题意舍去），

（Ⅱ）若点M落在∠BAC的平分线上，则有MG＝MF，即，解得x＝，

（Ⅲ）若点M落在∠ABC的平分线上，则有MH＝MF，即，解得x＝．

综合以上可得，当x＝或x＝时，点M落在△ABC的某条角平分线上．

②当0＜x≤3时，点M不在三角形外，△DME与△ABC重叠部分面积为△DME的面积，

∴，

当x＝3时，S的最大值为．

当3＜x≤6时，点M在三角形外，如图2，

由①知CM＝2CQ＝，

∴MT＝CM﹣CF＝，

∵PK//DE，

∴△MPK∽△MDE，

∴ ，

∴，

∵，

∴，

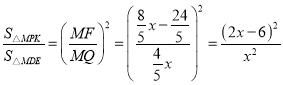即：，

∴当x＝4时，△DME与△ABC重叠部分面积的最大值为8．

综合可得，当x＝4时，△DME与△ABC重叠部分面积的最大值为8．