题目内容
【题目】某玩具商店以每件60元为成本购进一批新型玩具,以每件100元的价格销售则每天可卖出20件,为了扩大销售,增加盈利,尽快减少库存,商店决定采取适当的降价措施,经调查发现:若每件玩具每降价1元,则每天可多卖2件.
(1)若商店打算每天盈利1200元,每件玩具的售价应定为多少元?
(2)若商店为追求效益最大化,每件玩具的售价定为多少元时,商店每天盈利最多?最多盈利多少元?
【答案】(1)每件玩具的售价为80元;(2)每件玩具的售价为85元时,每天盈利最多,最多盈利1250元.
【解析】
(1)根据题意,可以得到关于x的一元二次方程,从而可以解答本题;
(2)根据题意可以得到利润与售价的函数关系式,然后根据二次函数的性质即可解答本题.
解:(1)设每件玩具的售价为![]() 元,
元,
![]() ,解得:
,解得:![]() ,
,![]() ,
,
∵扩大销售,增加盈利,尽快减少库存,∴![]() ,
,
答:每件玩具的售价为80元;
(2)设每件玩具的售价为![]() 元时,利润为
元时,利润为![]() 元,
元,
![]() ,
,
即当![]() 时,
时,![]() 有最大值为1250元,
有最大值为1250元,
答:当每件玩具的售价为85元时,商店每天盈利最多,最多盈利1250元.

练习册系列答案
相关题目
【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式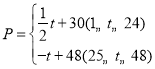 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?