题目内容
已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.

(1)求证:△ACE≌△ABD;
(2)若AC=2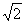 ,CD=1,求ED的长.
,CD=1,求ED的长.

(1)求证:△ACE≌△ABD;
(2)若AC=2
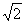 ,CD=1,求ED的长.
,CD=1,求ED的长.(1)根据等腰直角三角形的性质可得AB=AC,∠BAC=90°,AB=AE,∠CAE=90°,再根据同角的余角相等可得∠1=∠2,即可证得结论;(2)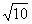
试题分析:(1)根据等腰直角三角形的性质可得AB=AC,∠BAC=90°,AB=AE,∠CAE=90°,再根据同角的余角相等可得∠1=∠2,即可证得结论;
(2)在△ABC中,根据∠B的正弦函数求得BC的长,即可得到BD的长,根据等腰直角三角形的性质可得∠4=∠B=45°,由△ACE≌△ABD可得∠5=∠B=45°,EC=DB=3,即可得到△ECD是直角三角形,最后根据勾股定理求解即可.
(1)∵△ABC是等腰直角三角形
∴AB=AC,∠BAC=90°
同理AB=AE,∠CAE=90°

∵∠BAC=∠CAE=90°
∴∠1+∠3=∠2+∠3=90°
∴∠1=∠2
∴△ACE≌△ABD(SAS)
(2)在△ABC中
BC=

∴BD=BC-CD=4-1=3
∵△ABC是等腰直角三角形
∴∠4=∠B=45°
∵△ACE≌△ABD
∴∠5=∠B=45°,EC=DB=3
∵∠ECD=∠4+∠5=90°
∴△ECD是直角三角形
∴ED
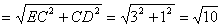 .
.点评:全等三角形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
相关题目