题目内容
如图,△ABC是边长为5的等边三角形,将△ABC绕点C顺时针旋转120°,得到△EDC,连接BD,交AC于F.
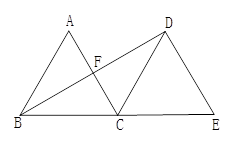
(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.

(1)猜想AC与BD的位置关系,并证明你的结论;
(2)求线段BD的长.
(1)证明四边形ABCD为菱形,从而得AC与BD互相垂直平分 (2)5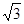
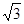
试题分析:(1)AC与BD互相垂直平分.
证明:连接AD,由题意知,△ABC≌△EDC,∠ACE=120°,
又∵△ABC是等边三角形,∴AB=DC=BC=DE=5,∠ABC=∠ACB=∠DCE=∠E=60°,
∴∠ACE+∠ACB=120°+60°=180°,∴B、C、E三点在一条直线上.
∴AB∥DC,∴四边形ABCD为菱形,∴AC与BD互相垂直平分.
(2)由(1)知,四边形ABCD为菱形,∴∠DBE=
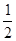 ∠ABC=30°,
∠ABC=30°,∵∠DBE+∠BDE+∠E=180°,∴∠BDE=90°.
∵ B、C、E三点在一条直线上,∴BE=10,
∴ BD=
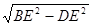 =
= =5
=5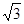
点评:本题考查菱形和勾股定理,掌握菱形的判定方法和菱形的性质是解本题的关键,熟悉勾股定理的内容

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 绕点C逆时针旋转角
绕点C逆时针旋转角 得
得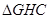 ,连结
,连结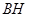 、
、 .
.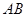 于点D,
于点D,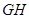 交
交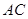 于点E、点F.
于点E、点F.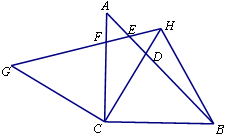
 全等除外);
全等除外); 是等腰三角形时,求
是等腰三角形时,求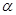 .
.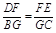 .
.
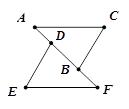

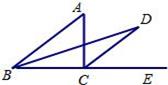

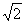 ,CD=1,求ED的长.
,CD=1,求ED的长. 的两条高线的长分别为5和20, 若第三条高线的长也是整数,则第三条高线长的最大值为 _______ .
的两条高线的长分别为5和20, 若第三条高线的长也是整数,则第三条高线长的最大值为 _______ .