Question

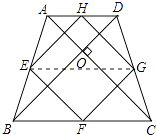
【题目】如图，在梯形ABCD中，AD∥BC，AB=DC，对角线AC、BD交于点O，AC⊥BD，E、F、G、H分别是AB、BC、CD、DA的中点．
（1）求证：四边形EFGH是正方形；
（2）若AD=2，BC=4，求四边形EFGH的面积．

Answer 1

【答案】
（1）证明：在△ABC中，E、F分别是AB、BC的中点，

故可得：EF= AC，同理FG= BD，GH= AC，HE= BD，

在梯形ABCD中，AB=DC，

故AC=BD，

∴EF=FG=GH=HE，

∴四边形EFGH是菱形．

在△ABD中，E、H分别是AB、AD的中点，

则EH∥BD，

同理GH∥AC，

又∵AC⊥BD，

∴EH⊥HG，

∴四边形EFGH是正方形．

（2）解：连接EG．

在梯形ABCD中，

∵E、G分别是AB、DC的中点，

∴EG是梯形的中位线，

∴EG= （AD+BC）=3．

在Rt△EHG中，

∵EH2+GH2=EG2，EH=GH，

∴EH2= ，即四边形EFGH的面积为

【解析】（1）先由三角形的中位线定理求出四边相等，然后由AC⊥BD入手，进行正方形的判断．（2）连接EG，利用梯形的中位线定理求出EG的长，然后结合（1）的结论求出EH2= ，也即得出了正方形EHGF的面积．
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握三角形中位线定理(连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半)的相关知识才是答题的关键．