题目内容
【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角, ①若AB是⊙O的直径,则∠APB=°;②若⊙O的半径是1,AB= ![]() ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系. 
【答案】
(1)90;45°或135°
(2)解:根据点P在⊙O1上的位置分为以下四种情况.
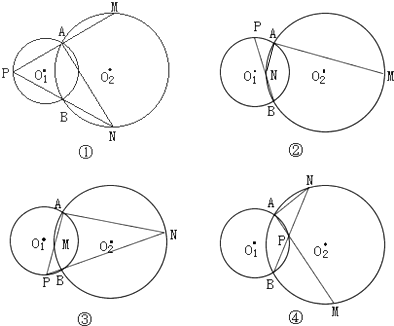
第一种情况:点P在⊙O2外,且点A在点P与点M之间,点B在点P与点N之间,如图①
∵∠MAN=∠APB+∠ANB,
∴∠APB=∠MAN﹣∠ANB;
第二种情况:点P在⊙O2外,且点A在点P与点M之间,点N在点P与点B之间,如图②.
∵∠MAN=∠APB+∠ANP=∠APB+(180°﹣∠ANB),
∴∠APB=∠MAN+∠ANB﹣180°;
第三种情况:点P在⊙O2外,且点M在点P与点A之间,点B在点P与点N之间,如图③.
∵∠APB+∠ANB+∠MAN=180°,
∴∠APB=180°﹣∠MAN﹣∠ANB,
第四种情况:点P在⊙O2内,如图④,
∠APB=∠MAN+∠ANB
【解析】解:(1)①若AB是⊙O的直径,则∠APB=90. ②解:如图,连接AB、OA、OB.
在△AOB中,
∵OA=OB=1.AB= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() .
.
∴∠AOB=90°.
当点P在优弧 ![]() 上时,∠APB= ∠AOB=45°;
上时,∠APB= ∠AOB=45°;
当点P在劣弧 ![]() 上时,∠AP′B= (360°﹣∠AOB)=135°
上时,∠AP′B= (360°﹣∠AOB)=135°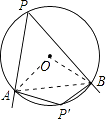
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
组别 | 垫球个数x(个) | 频数(人数) | 频率 |
1 | 10≤x<20 | 5 | 0.10 |
2 | 20≤x<30 | a | 0.18 |
3 | 30≤x<40 | 20 | b |
4 | 40≤x<50 | 16 | 0.32 |
合计 | 1 |
(1)表中a= , b=;
(2)这个样本数据的中位数在第组;
(3)下表为≤体育与健康≥中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有500名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人? 排球30秒对墙垫球的中考评分标准
分值 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
排球(个) | 40 | 36 | 33 | 30 | 27 | 23 | 19 | 15 | 11 | 7 |