Question

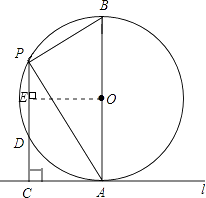
【题目】如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4）．
（1）当x= 时，求弦PA、PB的长度；
（2）当x为何值时，PDCD的值最大？最大值是多少？

Answer 1

【答案】
（1）解：∵⊙O与直线l相切于点A，且AB为⊙O的直径，

∴AB⊥l，又∵PC⊥l，

∴AB∥PC，

∴∠CPA=∠PAB，

∵AB是⊙O的直径，

∴∠APB=90°，又PC⊥l，

∴∠PCA=∠APB=90°，

∴△PCA∽△APB，

∴ ，即PA2=PCAB，

∵PC= ，AB=4，

∴PA= = ，

∴Rt△APB中，AB=4，PA= ，

由勾股定理得：PB= =

（2）解：过O作OE⊥PD，垂足为E，

∵PD是⊙O的弦，OE⊥PD，

∴PE=ED，

又∵∠CEO=∠ECA=∠OAC=90°，

∴四边形OACE为矩形，

∴CE=OA=2，又PC=x，

∴PE=ED=PC﹣CE=x﹣2，

∴PD=2（x﹣2），

∴CD=PC﹣PD=x﹣2（x﹣2）=x﹣2x+4=4﹣x，

∴PDCD=2（x﹣2）（4﹣x）=﹣2x2+12x﹣16=﹣2（x﹣3）2+2，

∵2＜x＜4，

∴当x=3时，PDCD的值最大，最大值是2．

【解析】（1）由直线l与圆相切于点A，且AB为圆的直径，根据切线的性质得到AB垂直于直线l，又PC垂直于直线l，根据垂直于同一条直线的两直线平行，得到AB与PC平行，根据两直线平行内错角相等得到一对内错角相等，再由一对直角相等，利用两对对应角相等的两三角形相似可得出△PCA与△PAB相似，由相似得比例，将PC及直径AB的长代入求出PA的长，在直角三角形PAB中，由AB及PA的长，利用勾股定理即可求出PB的长；（2）过O作OE垂直于PD，与PD交于点E，由垂径定理得到E为PD的中点，再由三个角为直角的四边形为矩形得到OACE为矩形，根据矩形的对边相等，可得出EC=OA=2，用PC﹣EC的长表示出PE，根据PD=2PE表示出PD，再由PC﹣PD表示出CD，代入所求的式子中，整理后得到关于x的二次函数，配方后根据自变量x的范围，利用二次函数的性质即可求出所求式子的最大值及此时x的取值．
【考点精析】通过灵活运用二次函数的最值和勾股定理的概念，掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题．