题目内容
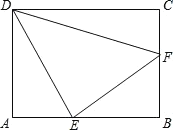
【题目】如图,长方形ABCD中,AB=4,AD=3,E是边AB上一点(不与A. B重合),F是边BC上一点(不与B. C重合).若△DEF和△BEF是相似三角形,则CF的长度为( ).
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或1
或1
【答案】C
【解析】
分①∠DEF=90°时,设AE=x,表示出BE=4-x,然后根据△ADE和△BEF相似,根据相似三角形对应边成比例可得![]() ,再根据相似三角形的邻边之比分两种情况列式求出x的值,然后求出BE,再求出BF、CF的值即可得解;②∠DFE=90°时,设CF=x,然后根据△BEF和△CFD相似,根据相似三角形对应边成比例可得
,再根据相似三角形的邻边之比分两种情况列式求出x的值,然后求出BE,再求出BF、CF的值即可得解;②∠DFE=90°时,设CF=x,然后根据△BEF和△CFD相似,根据相似三角形对应边成比例可得![]() ,再根据相似三角形的邻边之比分两种情况列式求出x的值,即可得解.
,再根据相似三角形的邻边之比分两种情况列式求出x的值,即可得解.
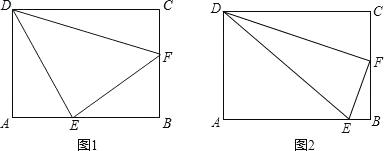
①如图1,∠DEF=90°时,设AE=x,则BE=4x,
易求△ADE∽△BEF,
∴![]() ,
,
即![]() ,
,
∵△DEF和△BEF是相似三角形,
∴△DEF和△ADE是相似三角形,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
整理得,6x=12或![]() (无解),
(无解),
解得x=2,
∴BE=42=2,
![]() ,
,
解得BF=![]() ,
,
CF=![]() ;
;
②如图2,∠DFE=90°时,设CF=x,则BF=3x,
易求△BEF∽△CFD,
∴![]() ,
,
即![]() ,
,
∵△DEF和△BEF是相似三角形,
∴△DEF和△DCF是相似三角形,
∴![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
整理得,8x=12或![]() =0(无解),
=0(无解),
解得![]() ;
;
综上所述,CF的值为![]() 或
或![]() .
.
故答案为:C

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目