题目内容
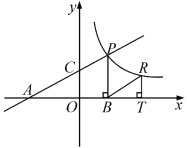
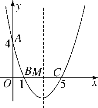
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2-
x2-![]() x+4,x=3;(2)
x+4,x=3;(2)![]() ;(3)N(
;(3)N(![]() ,-3).
,-3).
【解析】
(1)抛物线经过点A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解析式为y=a(x-1)(x-5),代入A(0,4)即可求得函数的解析式,则可求得抛物线的对称轴;
(2)点A关于对称轴的对称点A′的坐标为(6,4),连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小,可求出直线BA′的解析式,即可得出点P的坐标.
(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,![]() t2-
t2-![]() t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
解:(1) 根据已知条件可设抛物线的解析式为y=a(x-1)(x-5),
把点A(0,4)代入上式得:a=![]() ,∴y=
,∴y=![]() (x-1)(x-5)=
(x-1)(x-5)=![]() x2-
x2-![]() x+4=
x+4=![]() (x-3)2-
(x-3)2-![]() ,
,
∴抛物线的对称轴是:直线x=3;
即:抛物线的解析式为y=![]() x2-
x2-![]() x+4,抛物线的对称轴是x=3;
x+4,抛物线的对称轴是x=3;
(2)P点坐标为(3,![]() ).理由如下:
).理由如下:
∵点A(0,4),抛物线的对称轴是直线x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4)
如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.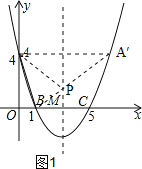
设直线BA′的解析式为y=kx+b,
把A′(6,4),B(1,0)代入得![]()
解得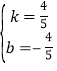
∴y=![]() x-
x-![]() ,
,
∵点P的横坐标为3,
∴y=![]() ×3-
×3-![]() =
=![]()
∴![]() ;
;
(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t, ![]() t2-
t2-![]() t+4)(0<t<5),如图,过点N作NG∥y轴交AC于G;作AD⊥NG于D,由点A(0,4)和点C(5,0)可求出直线AC的解析式为y=-
t+4)(0<t<5),如图,过点N作NG∥y轴交AC于G;作AD⊥NG于D,由点A(0,4)和点C(5,0)可求出直线AC的解析式为y=-![]() x+4,把x=t代入得y=-
x+4,把x=t代入得y=-![]() t+4,则G(t,-
t+4,则G(t,-![]() +4),此时NG=-
+4),此时NG=-![]() t+4-(
t+4-(![]() t2-
t2-![]() t+4)=-
t+4)=-![]() t2+4t,
t2+4t,
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CGN=![]() AD×NG+
AD×NG+![]() NG×CF=
NG×CF=![]() NG·OC=
NG·OC=![]() ×(-
×(-![]() t2+4t)×5=-2t2+10t=-2(t-
t2+4t)×5=-2t2+10t=-2(t-![]() )2+
)2+![]() ,
,
∴当t=![]() 时,△CAN面积的最大值为
时,△CAN面积的最大值为![]() ,由t=
,由t=![]() ,得y=
,得y=![]() t2-
t2-![]() t+4=-3,∴N(
t+4=-3,∴N(![]() ,-3).
,-3).