Question

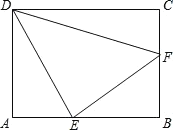
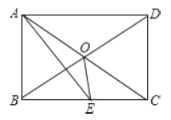
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE＝DC．以直线AB为对称轴的抛物线过C，E两点．点M为直线AB上一动点，点N为抛物线上一动点，当以点M，N，D，E为顶点的四边形是平行四边形时点N的坐标为___________．

Answer 1

【答案】（2，）或（0，2）或（2，1）

【解析】

分三种情况讨论：N在抛物线顶点处；N在抛物线对称轴左侧；N在抛物线对称轴右侧．

解：∵AB为抛物线的对称轴，

∴设抛物线的解析式为，

∵正方形OABC边长为2

∴h=2，

∵经过C（0，2）和E两点，

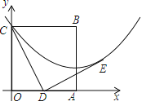
过点E作EF⊥x轴于点F，如图1，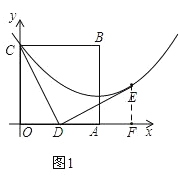

∵DE⊥DC，
∴∠CDO+∠EDF=90°，
∵∠CDO+∠OCD=90°，
∴∠OCD=∠EDF，
在△COD和△DFE中

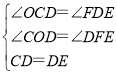
∴△COD≌△DFE（AAS），
∴OD=EF，DF=CO，
∵CO=OA=2，D为OA中点，
∴EF=OD=DA=1，DF=OC=2，
∴E（3，1）；

∴C（0，2）和E（3，1）两点代入，

得： ，解得：

∴抛物线的解析式为，

∴点N为抛物线上一动点，当以点M，N，D，E为顶点的四边形是平行四边形时点N的坐标可以分三种情况讨论：

（1） N在抛物线顶点处时，如图2所示，

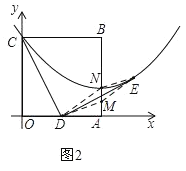
此时，N点就是抛物线的顶点（2，）；

（2）当N在抛物线对称轴左侧时，

过点C作CM∥DE交抛物线对称轴于点M，连接ME，如图3，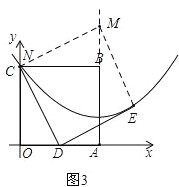

∵CM∥DE，DE⊥CD，
∴CM⊥CD，
∵OC⊥CB，
∴∠OCD=∠BCM，
在△OCD和△BCM中

∴△OCD≌△BCM（ASA），
∴CM=CD=DE，BM=OD=1，
∴CDEM是平行四边形，
即N点与C占重合，

∴N（0，2），

（3）N在抛物线对称轴右侧时，

N点在抛物线对称轴右侧，MN∥DE，如图4，

作NG⊥BA于点，延长DM交BN于点H，
∵MNED是平行四边形，
∴∠MDE=MNE，∠ENH=∠DHB，
∵BN∥DF，
∴∠ADH=∠DHB=∠ENH，
∴∠MNB=∠EDF，
在△BMN和△FED中

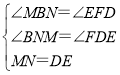
∴△BMN≌△FED（AAS），
∴BM=EF=1，
BN=DF=2，
∴M（2，1），

综上所述，点N的坐标为：（2，）或（0，2）或（2，1）