题目内容
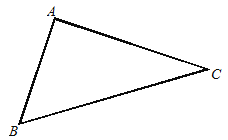
【题目】如图10,在三角形ABC中,∠BAC=90°.
(1)按下列要求画出相应的图形.
① 取线段BC的中点D,连接AD;
② 过点D分别画DE⊥AB,DF⊥AC,垂足分别为点E、F;
(2)在(1)所画出的图形中,按要求完成下列问题.
① 点A、D之间的距离是线段 的长;点D到AB的距离是线段 的长,约等于 mm(精确到1mm);
② ∠EDF= 度;
③ 三角形ABD与三角形ADC的面积有怎样的关系?为什么?
【答案】答案见解析
【解析】试题分析:(1)①用刻度尺量出线段BC的长度,算出BC的中点D,用线段连接A、D即可;②利用三角尺的两条直角边画出垂线;
(2)①根据两点间的距离和点到直线的距离解答,用刻度尺量出DE的长;②由四边形的内角和可求出∠EDF度数;③根据三角形的面积公式计算即可.
(1)①②如图1所示;
(2)① AD;DE,20(允许误差范围20±3)
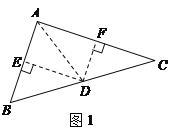
②∠EDF =360°-90°-90°-90°=90.
③ 三角形ABD与三角形ADC的面积相等,因为三角形ABD和三角形ADC分别以BD、DC为底,且BD=DC,高是点A到BC的距离,所以两三角形面积相等20mm.

练习册系列答案
相关题目