题目内容
【题目】如图,AB是⊙O的直径, AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP 、AF.
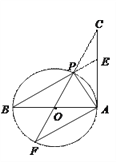
求证:(1)AF∥BE;(2)△ACP ∽△FCA.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析: (1)由∠B、∠F同对劣弧AP,可知两角的关系,又因BO=PO,△BOP是等腰三角形,求出∠F=∠BPF,得出结论;
(2)AC切 O于点A,AB是 O的直径,证明∠EAP=∠B,故△ACP∽△FCA;
试题解析:
(1)∵AB、PF为⊙O直径
∴OF=OA
∴∠F=∠FAB
∵∠F=∠B
∴∠B=∠FAB
∴AF∥BE
(2)∵AC为⊙O切线
∴∠CAB=90°
即∠PAC+∠PAB=90°
又∵PF为直径
∴∠FAB+∠PAB=90°
∴∠PAC=∠FAB
∵∠F=∠FAB
∴∠PAC=∠F
又∵∠C=∠C
∴△ACP ∽△FCA

练习册系列答案
相关题目