题目内容
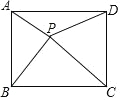
【题目】如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4以下判断:①PA+PB+PC+PD的最小值为10;②若△PAB≌△PDC,则△PAD≌△PBC;③若S1=S2,则S3=S4;④若△PAB∽△PDA,则PA=2.4;其中正确的是_______.
【答案】①③④
【解析】
①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理可得PA+PB+PC+PD的最小值,即可判断;
②若△PAB≌△PDC,则PA=PD,PB=PC,所以P在线段AD、BC的垂直平分线上,无法判断△PAD≌△PBC,故②错误;
③易证S1+S3=S2+S4,所以若S1=S2,则S3=S4,即可判断;
④根据相似三角形的性质可得∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,利用三角形内角和定理得出∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,即B、P、D三点共线,根据三角形面积公式可得PA=2.4,即可判断.
①当点P是矩形ABCD两对角线的交点时,PA+PB+PC+PD的值最小,根据勾股定理得,AC=BD=5,所以PA+PB+PC+PD的最小值为10,故①正确;
②若△PAB≌△PDC,则PA=PD,PB=PC,所以P在线段AD、BC的垂直平分线上,无法判断△PAD≌△PBC,故②错误;
③若S1=S2,易证S1+S3=S2+S4,则S3=S4,故③正确;
④若△PAB~△PDA,则∠PAB=∠PDA,∠PAB+∠PAD=∠PDA+∠PAD=90°,∠APD=180°-(∠PDA+∠PAD)=90°,同理可得∠APB=90°,那么∠BPD=180°,B、P、D三点共线,P是直角△BAD斜边上的高,根据面积公式可得PA=2.4,故④正确.
故答案为①③④.