题目内容
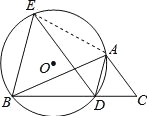
【题目】如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.
(1)求证:ED∥AC;
(2)连接AE,试证明:ABCD=AEAC.

【答案】(1)证明详见解析;(2)证明详见解析.
【解析】
试题分析:(1)由圆周角定理,可得∠BAD=∠E,又由BE∥AD,易证得∠BAD=∠ADE,然后由AD是△ABC的角平分线,证得∠CAD=∠ADE,继而证得结论;
(2)首先连接AE,易得∠CAD=∠ABE,∠ADC=∠AEB,则可证得△ADC∽△BEA,然后由相似三角形的对应边成比例,证得结论.
试题解析:(1)∵BE∥AD,
∴∠E=∠ADE,
∵∠BAD=∠E,
∴∠BAD=∠ADE,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠CAD=∠ADE,
∴ED∥AC;
(2)连接AE,
∵∠CAD=∠ADE,∠ADE=∠ABE,
∴∠CAD=∠ABE,
∵∠ADC+∠ADB=180°,∠ADB+∠AEB=180°,
∴∠ADC=∠AEB,
∴△ADC∽△BEA,
∴AC:AB=CD:AE,
∴ABCD=AEAC.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目




