题目内容
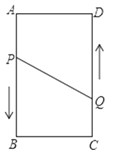
【题目】如图①，正方形ABCD，点E，F分别在AB，CD上，DG⊥EF于点 H．
（1）求证：DG＝EF；
（2）在图①的基础上连接AH，如图②，若 AH＝AD，试确定DF与 CG的数量关系，并说明理由；
（3）在（2）的条件下，作∠FEK＝45°，点 K在 BC边上，如图③，若AE＝KG＝2，求EK的长．
【答案】（1）证明见解析；（2）DF＝2GC；（3）
.
【解析】
（1）过点F作FM⊥AB于点M，由题意可证MF=BC=CD，∠BEF=∠DFE=∠DGC，即可证△EFM≌△GDC，即可得EF=DG；
（2）过点A作AM⊥DG于点M，过点C作CN⊥DG于点N．由题意可证△ADM≌△DCN，可得DM=CN=
DH，由题意可证△DFH∽△DGC，可得
＝2，即可得DF=2CG
（3）过点F作FM⊥AB，连接MK，FK，由题意可证Rt△EMF≌Rt△GCD，可求EM=GC，由AM=DF=2GC，可得GC=EM=2，则可证点E，点F，点K，点M四点共圆，可得∠EMF=∠EKF=90°，可证△BEK≌△CKF，可得CK=BE=4，BM=2=BK，根据勾股定理可求EK的长．
（1）证明：过点F作FM⊥AB于点M，
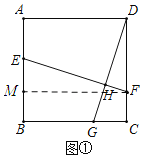
∵四边形ABCD是正方形，
∴∠B=∠C=90°，AB=BC=CD，AB∥CD
∵FM⊥AB，∠B=∠C=90°
∴四边形BCFM是矩形
∴MF=BC
即MF=CD
∵EF⊥DG，
∠C=90°
∴∠CDG+∠DGC=90°，∠CDG+∠DFE=90°
∴∠DGC=∠DFE
∵AB∥CD
∴∠BEF=∠EFD
∴∠BEF=∠DGC，且MF=CD，∠EMF=∠C=90°
∴△EFM≌△GDC（AAS）
∴EF=GD
（2）DF=2GC
过点A作AM⊥DG于点M，过点C作CN⊥DG于点N．
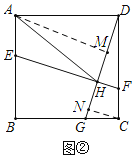
∵CN⊥DG，∠ADC=90°
∴∠ADG+∠GDC=90°，∠GDC+∠NCD=90°
∴∠ADG=∠DCN
∵AD=AH，AM⊥DG
∴MD=MH=DH，
∵AD=CD，∠AMD=∠CND=90°，∠ADG=∠NCD
∴△ADM≌△DCN（AAS）
∴MD=NC
即DH=2NC
∵∠DGC=∠DFE，∠DHF=∠DCG=90°
∴△DFH∽△DGC
∴＝2
∴DF=2GC
（3）如图：过点F作FM⊥AB，连接MK，FK，
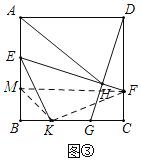
∵FM⊥AB，∠B=∠C=∠BAD=∠ADC=90°
∴四边形ADFM是矩形，四边形BCFM是矩形
∴DF=AM，AD=MF=BC=CD，
∵EF=DG，MF=CD
∴Rt△EMF≌Rt△GCD（HL）
∴GC=EM
∵DF=2GC
∴AM=2GC=2EM
∴AE=EM=2=CG
∴DF=4=CK
∴BK=BM
∴∠BMK=∠BKM=45°
∴∠FMK=45°
∵∠FMK=∠FEK=45°
∴点E，点F，点K，点M四点共圆
∴∠EMF=∠EKF=90°
∴∠FEK=∠EFK=45°
∴EK=FK，
∵∠BEK+∠EKB=90°，∠FKC+∠EKB=90°
∴∠FKC=∠BEK，且∠B=∠C=90°，EK=FK
∴△BEK≌△CKF（AAS）
∴CK=BE=4
∴BM=2=BK
∴EK=
.
