题目内容
【题目】如图，已知直线y＝﹣2x经过点P（﹣2，a），点P关于y轴的对称点P′在反比例函数y＝
（k≠0）的图象上．
（1）求反比例函数的解析式；
（2）直接写出当y＜4时x的取值范围．
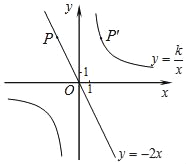
【答案】（1）y=
；（2）反比例函数自变量x的范围为x＞2或x＜0；一次函数自变量x的范围是x＞-2
【解析】
(1)把P的坐标代入直线的解析式，即可求得P的坐标，然后根据关于y轴对称的两个点之间的关系，即可求得P'的坐标，然后利用待定系数法即可求得反比例函数的解析式；
（2）根据反比例函数的增减性即可求得x的范围．
（1）把P（﹣2，a）代入直线y=-2x解析式得：a=4，即P（﹣2，4），
∴点P关于y轴对称点P′为（2，4），
代入反比例解析式得：k=8，
则反比例解析式为y=
；
（2）当y＜4时，反比例函数自变量x的范围为x＞2或x＜0；一次函数自变量x的范围是x＞-2．
练习册系列答案
相关题目
【题目】王勇和李明两位同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了30次实验，实验的结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
（1）分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率；
（2）王勇说：“根据以上实验可以得出结论：由于5点朝上的频率最大，所以一次实验中出现5点朝上的概率最大”；李明说：“如果投掷300次，那么出现6点朝上的次数正好是30次”．试分别说明王勇和李明的说法正确吗？并简述理由；
（3）现王勇和李明各投掷一枚骰子，请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率．
