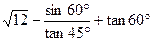题目内容
若一个等腰三角形的两边长分别为2cm和6cm，则底边上的高为__________cm，底角的余弦值为__________。
，
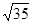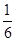
分析：根据组成三角形的三边条件可确定等腰三角形的腰和边的长；作底边上的高，构造直角三角形，运用三角函数定义求解．
解答：解：∵三角形的两边之和大于第三边，
∴等腰三角形的腰只能是6，
∴底边为2，
作底边的高，利用勾股定理得，
高h=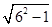
=
；
底角的余弦值cosα=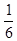
．
解答：解：∵三角形的两边之和大于第三边，
∴等腰三角形的腰只能是6，
∴底边为2，
作底边的高，利用勾股定理得，
高h=
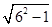=；底角的余弦值cosα=
．
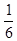练习册系列答案
手拉手全优练考卷系列答案
相关题目
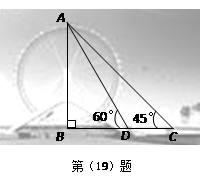
,∠ABC=45o，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使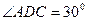
（如图所示）．
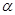的边OA上一点，且P点的坐标为（3，4），则sin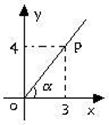
≈1.73，计算结果保留整数)
，
，
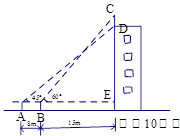
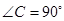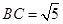，则∠A的度数为（ ）。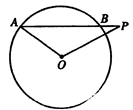
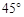，再往摩天轮的方向前进50 m至D处，测得最高点A的仰角为
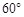．求该兴趣小组测得的摩天轮的高度AB
