题目内容
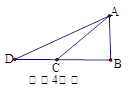
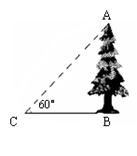
如图,根据所示图形中所给的数据求得CD高度约为 m。( ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)
 ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)
3米
分析:首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
解答:解:∵AB=8,BE=15,∴AE=23,在Rt△AED中,∠DAE=45°,∴DE=AE=23.
在Rt△BEC中,∠CBE=60°,∴CE=BE?tan60°=15 ,∴CD=CE-DE=15
,∴CD=CE-DE=15 -23≈2.95≈3
-23≈2.95≈3
即这块广告牌的高度约为3米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.
解答:解:∵AB=8,BE=15,∴AE=23,在Rt△AED中,∠DAE=45°,∴DE=AE=23.
在Rt△BEC中,∠CBE=60°,∴CE=BE?tan60°=15
 ,∴CD=CE-DE=15
,∴CD=CE-DE=15 -23≈2.95≈3
-23≈2.95≈3即这块广告牌的高度约为3米.
点评:本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目





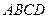 中,点
中,点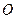 在对角线
在对角线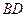 上,以
上,以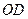 的长为半径的⊙
的长为半径的⊙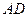 ,
,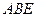 =∠
=∠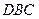 .
.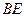 与⊙
与⊙
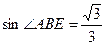 ,
,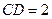 ,求⊙
,求⊙ )
) +(-1)
+(-1)