题目内容
【题目】数轴上有![]() 、
、![]() 、
、![]() 三个点,分别表示有理数
三个点,分别表示有理数![]() 、
、![]() 、
、![]() ,两条动线段
,两条动线段![]() 和
和![]() ,
,![]() ,
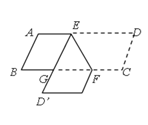
,![]() ,如图,线段
,如图,线段![]() 以每秒
以每秒![]() 个单位的速度从点
个单位的速度从点![]() 开始一直向右匀速运动,线段
开始一直向右匀速运动,线段![]() 同时以每秒
同时以每秒![]() 个单位的速度从点
个单位的速度从点![]() 开始向右匀速运动,当点
开始向右匀速运动,当点![]() 运动到
运动到![]() 时,线段
时,线段![]() 立即以相同的速度返回,当点
立即以相同的速度返回,当点![]() 运动到点
运动到点![]() 时,线段
时,线段![]() 、
、![]() 立即同时停止运动,设运动时间为
立即同时停止运动,设运动时间为![]() 秒(整个运动过程中,线段
秒(整个运动过程中,线段![]() 和
和![]() 保持长度不变,且点
保持长度不变,且点![]() 总在点
总在点![]() 的左边,点
的左边,点![]() 总在点
总在点![]() 的左边)
的左边)

(1)当![]() 为何值时,点
为何值时,点![]() 和点
和点![]() 重合?
重合?
(2)在整个运动过程中,线段![]() 和
和![]() 重合部分长度能否为
重合部分长度能否为![]() ,若能,请求出此时点
,若能,请求出此时点![]() 表示的数;若不能,请说明理.
表示的数;若不能,请说明理.
【答案】(1)当![]() 或
或![]() 时,点
时,点![]() 和点
和点![]() 重合;(2)在
重合;(2)在![]() 和
和![]() 之间或在
之间或在![]() 和
和![]() 之间.
之间.
【解析】
(1)分两种情况讨论,追及时等量关系为:点![]() 行走的路程
行走的路程![]() 行走的路程
行走的路程![]() ;返回后相遇等量关系为:点
;返回后相遇等量关系为:点![]() 行走的路程
行走的路程![]() 行走的路程
行走的路程![]() ;
;
(2)分两种情况讨论,追及时点![]() 超过点
超过点![]() 一个单位长度和点
一个单位长度和点![]() 超过点
超过点![]() 一个单位长度时都符合线段
一个单位长度时都符合线段![]() 和
和![]() 重合部分长度能为
重合部分长度能为![]() ;返回后相遇时点
;返回后相遇时点![]() 离点
离点![]() 一个单位长度和点
一个单位长度和点![]() 离点
离点![]() 一个单位长度时都符合线段
一个单位长度时都符合线段![]() 和
和![]() 重合部分长度能为
重合部分长度能为![]() ;据此求得
;据此求得![]() 的值,从而求得点
的值,从而求得点![]() 的范围.
的范围.
(1)①追及时,依题意得:![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
②返回后相遇,依题意得:![]() 即:
即:![]() ,
,
解得:![]() ,
,
答:当![]() 或
或![]() 时,点
时,点![]() 和点
和点![]() 重合;
重合;
(2)①追及时点![]() 超过点
超过点![]() 一个单位长度:
一个单位长度:![]() ,即
,即![]() ,
,
解得:![]() ,
,
②追及时点![]() 超过点
超过点![]() 一个单位长度:
一个单位长度:![]() ,即
,即![]() ,
,
解得:![]() ,
,
即:![]() ,
,
∴点![]() 表示的数在
表示的数在![]() 和
和![]() 之间;
之间;
③返回后相遇时点![]() 离点
离点![]() 一个单位长度:
一个单位长度:![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
④返回后相遇时点![]() 离点
离点![]() 一个单位长度:
一个单位长度:![]() ,即:
,即:![]() ,
,
解得:![]() ,
,
∴点![]() 表示的数在
表示的数在![]() 和
和![]() 之间;
之间;
综上:点![]() 表示的数为:在
表示的数为:在![]() 和
和![]() 之间或在
之间或在![]() 和
和![]() 之间.
之间.

练习册系列答案
相关题目