题目内容
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
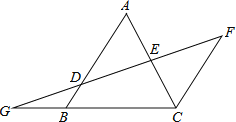
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
【答案】(1)证明见解析(2)4
【解析】
试题分析:(1)由平行线的性质可得:∠A=∠FCE,再根据对顶角相等以及全等三角形的判定方法即可证明:△ADE≌△CFE;
(2)由AB∥FC,可证明△GBD∽△GCF,根据给出的已知数据可求出CF的长,即AD的长,进而可求出AB的长.
(1)证明:∵AB∥FC,
∴∠A=∠FCE,
在△ADE和△CFE中,
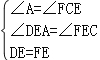 ,
,
∴△ADE≌△CFE(AAS);
(2)解:∵AB∥FC,
∴△GBD∽△GCF,
∴GB:GC=BD:CF,
∵GB=2,BC=4,BD=1,
∴2:6=1:CF,
∴CF=3,
∵AD=CF,
∴AB=AD+BD=4.

练习册系列答案
相关题目